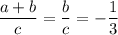Если множеством решений неравентсва ax^2+bx+c> 0 является интервал (3; +беск), то чему равно (a+b)/c? с объяснением
Другие вопросы по теме Алгебра
Популярные вопросы
- Контрольная по теме имя числительное шестиногие богатыри все...
3 - Кир булычев какие были выдвинуты лечения ивана ивановича...
2 - Определите и запишите лексическое значение слова голову из предложения...
3 - Квечеру, перед самыми сум..рками, проходил я по вознесенскому...
2 - Установітьвідповідність між формулою n-го члена (1-3) ї прогресії...
1 - 2\frac{2}{3}+2\frac{1}{3}\cdot \left(-15\frac{3}{7}-\left(-4,8\right)\div...
1 - 20 доказать что васютка из произведения васюткино озеро что он...
1 - Аксаков-певец природы напишите сочинение . 70...
1 - Сравните центральный тянь-шань с северным тянь-шанем. а) определите...
2 - Напишите, , сочинение на тему чем я больше всего люблю заниматься...
3
Вообще неравенство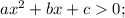 имеет либо два промежутка с бесконечностями на краях, либо один промежуток без бесконечностей, либо x∈R, если дискриминант отрицательный, а ветви вверх направлены, либо не имеет решений, если дискриминант неположительный (при D=0 парабола касается оси ОХ, но неравенство строгое). А здесь промежуток как при решении линейного неравенства.
имеет либо два промежутка с бесконечностями на краях, либо один промежуток без бесконечностей, либо x∈R, если дискриминант отрицательный, а ветви вверх направлены, либо не имеет решений, если дискриминант неположительный (при D=0 парабола касается оси ОХ, но неравенство строгое). А здесь промежуток как при решении линейного неравенства.
А оно может быть так, если a=0
Тогда имеем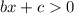
При
А вот при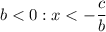 , это не годится.
, это не годится.
Учитывая, что а=0,