Если две корни(нули) неравенства встречается два раза то между этими корнями значение меняется с минуса на плюс?

Другие вопросы по теме Алгебра
Популярные вопросы
- 1. У котрому рядку всі слова мають однакову кількість звуків? А свято, з...
1 - (3целых-12/17+4целых-5/21) - 1 целая 12/17...
3 - Вопросы 1. Почему много стрекоз встречается у водоёмов?2. Каких жуков, встречающихся...
1 - ,переведите это предложение,переводчик не работает....
1 - Какая сила действует на пружину жесткостью 200 Ньютонов на метр если она...
2 - 1. Сұрақтарды көршіңмен талқыла. зергер деген – кім? Ол не істейді? Зергер...
1 - TESTForm 7 Term 21.Choose the appropriate verb forms to complete the sentences.1.He...
1 - Астана қала. Бүгінде Астананың аты әлемге әйгілі. Қазақ елі болашағының...
3 - Лінзу переміщують між нерухомими лампою Л та екраном Е. На екрані утворюється...
2 - Образ античної літератури який припав мені до душі...
1
Множители обращаются в 0 при х= -2, х=3 , х=1 , х= -1 .
Вычислим знак дроби в каждом из пяти промежутках. Для этого подставляем какое-либо число из промежутка вместо "х" в последнюю дробь.
Теперь выбираем промежутки, где стоит знак (-), т.к. у заданного неравенства знак "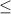 " .
" .
ответ:![x\in [\, -2\ ;\ -1\ )\cup (\ 1\, ;\ 3\ ]\ .](/tpl/images/1359/5619/4bb9c.png)
P.S. Считать знаки можно устно .