1. Алгебра
  2. Если для функции f(x)

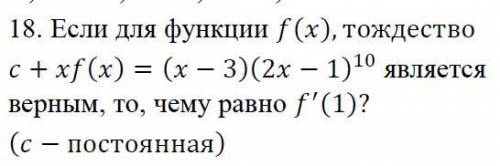
Если для функции f(x) выполняется равенство... Условия в приложении. Решить задачу.


Если для функции f(x) выполняется равенство... Условия в приложении. Решить задачу.

kurilov218 kurilov218    1   13.09.2020 02:19    4

Ответы
niloybasak0 niloybasak0  15.10.2020 20:33

c - 37

Объяснение:

Выразим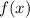 f(x) из данного тождества.

{\displaystyle f(x) = \frac{(x-3)(2x-1)^{10}-c}{x}

Найдем производную.

По формуле для частного:

{\displaystyle f'(x) = \frac{((x-3)(2x-1)^{10}-c)'*x-((x-3)(2x-1)^{10}-c)*x'}{x^2}

{\displaystyle ((x-3)(2x-1)^{10}-c)' = ((x-3)(2x-1)^{10})' - c' = ((x-3)(2x-1)^{10})' - 0

{\displaystyle ((x-3)(2x-1)^{10})' = (x-3)'(2x-1)^{10} + (x-3)((2x-1)^{10})'

{\displaystyle (x-3)' = x' - 3' = 1 - 0 = 1

Далее нужно вычислить производную сложной функции:

\displaystyle ((2x-1)^{10})' = 10 (2x-1)^9*(2x-1)' = 10 (2x-1)^9 * 2 = 20(2x-1)^9

Собираем все вместе:

{\displaystyle ((x-3)(2x-1)^{10})' = 1(2x-1)^{10} + 20(x-3)(2x-1)^9

{\displaystyle f'(x) = \frac{((2x-1)^{10} + 20(x-3)(2x-1)^9)*x-((x-3)(2x-1)^{10}-c)*1}{x^2}

Нужно найти лишь значение при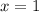 x=1 поэтому приводить к более красивому виду я не буду.

Найдем значение производной при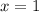 x=1

{\displaystyle f'(1) = \frac{((2-1)^{10} + 20(1-3)(2-1)^9)*1-((1-3)(2-1)^{10}-c)}{1^2} =

{\displaystyle = \frac{(1^{10} + 20(-2)1^9)-((-2)1^{10}-c)}{1} =

{\disaplystyle = 1 - 40 - (-2-c) = 1 - 40 + 2 + c = -37 + c = c - 37

Теория:

Правила дифференцирования:

Если С - постоянное число.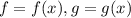 {\displaystyle f=f(x) , g = g(x) - некоторые дифференцируемые функции, то:

{\displaystyle C' = 0

{\displaystyle (x^n)' = nx^{n-1}

{\displaystyle (f \pm g)' = f' \pm g'

(fg)' = f'g+fg'

{\displaystyle \left(\frac{f}{g} = \frac{f'g-fg'}{g^2} \right)

{\displaystyle (f(g(x)))' = f(g)' * g(x)'

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
sonatap01f6p sonatap01f6p  22.09.2019 08:40
Разложить многочлен на множители. a) 100x^2 - 49y^2 б) 36a^2 + 12a + 1 решить уравнение. a) 3x^2 + x = 0 б) 49x - x^3 = 0...
89132508504 89132508504  22.09.2019 08:40
Разложить многочлен на множители. а) 100x^2 - 49y^2 б) 36а^2 + 12a + 1 решите уравнение. а) 3x^2 + x = 0 б) 49x - x^3 = 0...
olegohremenko olegohremenko  11.07.2019 18:00
Катет и гипотенуза прямоугольного треугольника равна 20 и 52 найдите высоту проведенную к гипотенузе...
Женечка5551 Женечка5551  11.07.2019 18:00
При якому значенні b графік функції y=-bx+3 проходить через точку а) (2; -6] б) (-2; 4)...
sveta7185684p0dufr sveta7185684p0dufr  11.07.2019 18:00
Постройте график функции,заданной формулой y=-2x+0,5 . заранее...
ksjsksskskjns ksjsksskskjns  11.07.2019 18:00
Постройте график уравнения 3x-5y-15=0 (x+3)(y-5)=0 xy-12=0 x^2+y^2=16 3|y|+x^2=0...
Fdcsxdxdvrcfcr Fdcsxdxdvrcfcr  11.07.2019 17:50
Решите систему и распишите подробно, ) система: 6a+18b-24=0, 4+4a+4b=0;...
IKarapuzikI IKarapuzikI  11.07.2019 17:50
Найдите сторону ромба,если его площадь равно 8 корень2см2,а угол 45 градусов...
lolkekpfff lolkekpfff  11.07.2019 17:50
Вкоробке лежат 2 красных , 4 зелёных и 10 синих карандашей какова вероятность того ,что наугад вынутый карандаш будет : 1) красным , 2) зелёным ,3) не зелёным ? какое наименьшее...
саша080706 саша080706  09.09.2019 05:20
Как решить данное уравнение? : (2x-0,1)+(3x-5)+7 как раскрыть скобки?...

Популярные вопросы