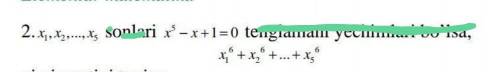
Алгебра: Если числа х1,х2..х5 , решение уравнениято найдите ...

Если числа х1,х2..х5 , решение уравнениято найдите ...

Ответы

Rapapapapap2212 27.08.2021 22:06

Уравнение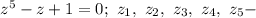 $z^5-z+1=0;\ z_1,\ z_2,\ z_3,\ z_4,\ z_5 -$ корни этого уравнения.

Требуется вычислить выражение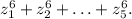 $z_1^6+z_2^6+\ldots + z_5^6.$ Заметим, что для любого корня уравнения выполнено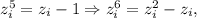 $z_i^5=z_i-1\Rightarrow z_i^6=z_i^2-z_i,$

поэтому сумма шестых степеней корней этого уравнения равна сумме вторых степеней минус сумма самих корней.

Теперь вступает в бой волшебник - великая теорема Виета. Вот ее формулировка, записанная в случае, когда старший коэффициент равен одному, а многочлен имеет пятую степень.

$f(z)=z^5+ a_4z^4+a_3z^3+a_2z^2+a_1z+a_0;\ z_1,\ z_2,\ z_3,\ z_4,\ z_5 -$ его корни.

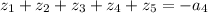1) Тогда z_1+z_2+z_3+z_4+z_5=-a_4 (сумма корней равна коэффициенту при четвертой степени, взятому с обратным знаком). В нашем случае этот коэффициент равен нулю, поэтому сумма корней равна нулю.

2)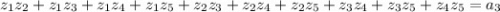 z_1z_2+z_1z_3+z_1z_4+z_1z_5+z_2z_3+z_2z_4+z_2z_5+z_3z_4+z_3z_5+z_4z_5=a_3 (сумма попарных произведений корней равна коэффициенту при третьей степени). В нашем случае этот коэффициент равен нулю, поэтому сумма попарных произведений корней равна нулю.

3) Сумма тройных произведений корней равна -a_2. В этой задаче нам это равенство не понадобится.

4) Сумма четверных произведений равна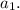 a_1. Это тоже нам не понадобится.

5)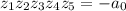 z_1z_2z_3z_4z_5=-a_0 (произведение корней равно свободному члену, взятому с обратным знаком). И это нам не понадобится.

Напоминаю, что мы уже доказали, что сумма корней равна нулю, остается разобраться с суммой квадратов корней. Напрямую теорема Виета ничего про эту сумму не говорит, но дело мастера боится. Имеем:

$(z_1+z_2+\ldots+z_5)^2=z_1^2+z_2^2+\ldots +z_5^2+2\sum\limits_{i\not= j}z_iz_j$

(то есть квадрат суммы равен сумме квадратов плюс удвоенная сумма попарных произведений - элементарное обобщение общеизвестной формулы (a+b)²=a²+b²+2ab). В нашем случае сумма корней и сумма попарных произведений корней равна нулю. Поэтому и сумма квадратов корней равна нулю.

А в общем случаен из теоремы Виета следовало бы, что

$z_1^2+z_2^2+\ldots+z_5^2=a_4^2-2a_3.$