Экскурсионный теплоход регулярно перемещается из пункта a в пункт b, расстояние между которыми 570 км. теплоход отправился с постоянной скоростью из a в b. после прибытия он отправился обратно со скоростью на 8 км/ч больше прежней, сделав по пути остановку на отдых на 4 часа. в результате теплоход затратил на обратный путь столько же времени, сколько на путь от a до b. найдите скорость теплохода на пути из a в b. ответ дайте в км/ч.
Другие вопросы по теме Алгебра
Популярные вопросы
- Знайти п ять перших членів числової послідовності (an) якщо an=3n+2...
2 - Постройте координатный луч приняв за единичный отрезок 12 см. отметьте на координатном...
2 - 1.Ділянка кола складається з трьох паралельно з єднаних резисторів, опорами...
2 - Напишите рецензию по рассказу шукшина чудик ответ желательно доступный языку...
3 - Написать программу, которая вводит массив из N вещественных чисел, а затем...
3 - Сколько существует видов блоков ...
3 - 1.какую опасность несли казахам джунгарские нашествия 2.оцените качества Тауке...
3 - Выберите точку принадлежащую графику функции у=-х+3 а)А(0;3) б)В(2,5;-0,5)...
1 - Какую религию объявил государственной религией князь Ягайло для Великого княжества...
2 - Неліктен АҚШ өз әскерм кемелепін Жапонияға жіберді...
3
Пусть скорость теплохода равна х км/ч из А в В, тогда в обратный путь из В в А скорость теплохода равна (x+8) км/ч. Время, затраченное в путь из А в В, равно 570/х, а в обратном направлении - 570/(x+8). На весь путь теплоход затратил 570/x - 570/(x+8), что составляет, по условию, 4 часа.
Составим уравнение и решим его.
По теореме Виета: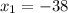 - не удовлетворяет условию.
- не удовлетворяет условию.
ответ: 30 км/ч.