Два робітники, працюючи разом, можуть виконати завдання на 8 год швидше, ніж один перший робітник і на 18 год швидше, ніж один другий. За скільки годин перший робітник може виконати завдання і за скільки - другий?
Другие вопросы по теме Алгебра
Популярные вопросы
- Племя мульти имеет 16 символьный алфавит. Племя пульти использует 128 символьный...
1 - Спряжение глагола sein в prasens 1.lch__schuler ( sind-bin-ist) 2.peter__mein...
3 -  Доклад по географии на тему природные ресурсы России и хозяйственная...
1 - Текст з англ мови на тему My shopping dayБажано з перекладом 8-10речень...
1 - Решите уравнение. В ответе укажите сумму корней....
2 - НЕ СПАМИТЬ, ПОТОМУ ЧТО ВСЕ РАВНО ЗАБЕРУ ЕСЛИ НАПИШИЕ ЧЕПУХУ sentences! Write...
3 - Можете даже половину решить. ...
3 - 6. Визначити географічну довготу середніх меридіанів таких поясів: а) нульовогоб)...
3 - Условие задания:3 Б. Приведи одночлены к стандартному виду и укажи те, у...
2 - (4 1/3+6,25-3,5):3 2/5-1 1/6: 7/8...
1
Нехай за год перший робітник виконає завдання, а за
год перший робітник виконає завдання, а за 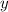 год — другий. Тоді за одну годину перший робітник виконає
год — другий. Тоді за одну годину перший робітник виконає  усього завдання, а другий робітник —
усього завдання, а другий робітник —  .
.
Два робітники, працюючи разом, можуть виконати завдання на 8 год швидше, ніж один перший робітник, тобто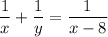
Два робітники, працюючи разом, можуть виконати завдання на 18 год швидше, ніж один другий робітник, тобто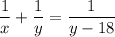
Складаємо систему з двох рівнянь:
Тут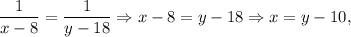 оскільки ліві частини рівнянь рівні.
оскільки ліві частини рівнянь рівні.
Підставимо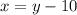 в перше рівняння:
в перше рівняння:
Якщо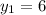 , то
, то 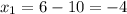 — не відповідає сенсу задачі.
— не відповідає сенсу задачі.
Якщо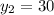 , то
, то 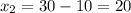
Отже, за 20 год перший робітник виконає завдання, а за 30 год — другий.
Відповідь: 20 год і 30 год.