Два ретроавтомобиля отправляются в 720-километровый пробег. первый едет со скоростью на 10км/ч больше,чем второй, и прибывает на 50 часов раньше

Question

Алгебра: Два ретроавтомобиля отправляются в 720-километровый пробег. первый едет со скоростью на 10км/ч больше,чем второй, и прибывает на 50 часов раньше второго. найдите скорость второго авто(км/ч)

akulkaeva78 · Answer

Пусть скорость второго автомобиля равна х км/ч, а первого — (х+10) км/ч. Время, затраченное первым автомобилем равно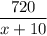 $\dfrac{720}{x+10}$ ч, а вторым — 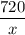$\dfrac{720}{x}$ . На весь путь они затратили 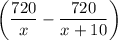$\bigg(\dfrac{720}{x}-\dfrac{720}{x+10}\bigg)$ ч, что по условию составляет 50 часов.

Составим и решим уравнение:

$\dfrac{720}{x}-\dfrac{720}{x+10}=50~~~\bigg|\cdot \dfrac{x}{10}(x+10)\ne 0\\ \\ 72(x+10)-72x=5x(x+10)\\ \\ 72x+720-72x=5x^2+50x\\ \\ 5x^2+50x-720=0~~|:5\\ \\ x^2+10x-144=0$