Два насоса работая вместе наполняют бассейн водой за 12 часов. за сколько часов может наполнить бассейн водой первый из насосов, работая отдельно, если известно, что половину бассейна он наполняет водой на 5 часов быстрее, чем второй насос?
Другие вопросы по теме Алгебра
Популярные вопросы
- 5. Найдите в тексте параграфа в космосе решать земные проблемы?...
2 - Доведіть що Маруся Богуслава дійсно українська героїня...
1 - Знайдіть об єднання і переріз числових поміжків [ 2;3 ] [ 3; 5)...
1 - Какие признаки характерны для генеративной почки: -содержит укороченный...
2 - Рассчитайте и зпаполните пустые ячейки в таблице...
2 - 5. . Төмендегі көмекші есімдермен сөйлем құра. Ортасында, артында,...
1 - Кот в сапогах характеристики героев...
3 - Обчислить площу Полное решение...
3 - 1) a/b = 13/5; НОД(a;b)=32) a/b = 7/8 ; НОК(a;b)=224...
3 - А.С.Пушкин. «Полтавский бой» Вопросы для учащихся. 1.Как рисуется стремительность...
1
ответ: 20 часов.
Объяснение: Пусть весь бассейн 1 (единица), тогда совместная производительность двух насосов будет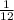 (бас/ч). Возьмем, что за х часов первый насос может наполнить весь бассейн самостоятельно, тогда его производительность будет
(бас/ч). Возьмем, что за х часов первый насос может наполнить весь бассейн самостоятельно, тогда его производительность будет 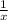 (бас/ч). Т.к. второй насос наполняет половину бассейна на 5 часов дольше, то целый бассейн он наполнит на 5÷(1/2)=10 часов дольше первого и соответственно производительность второго насоса будет
(бас/ч). Т.к. второй насос наполняет половину бассейна на 5 часов дольше, то целый бассейн он наполнит на 5÷(1/2)=10 часов дольше первого и соответственно производительность второго насоса будет 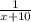 (бас/ч). Составим уравнение:
(бас/ч). Составим уравнение:
x₁=(-6) (ч) Не подходит, т.к. время не может быть отрицательное.
х₂=20 (ч) нужно первому насосу, чтобы наполнить бассейн водой, работая самостоятельно.