Два насоса, работая вместе, могут наполнить бассейн за 48 минут. за сколько минут может наполнить бассейн первый насос, работая один, если второму на эту работу нужно на 20 минут больше?
Другие вопросы по теме Алгебра
Популярные вопросы
- Птичка колибри массой 2 г при полете на высоту 1 м достигает скорость 180км/ч. определите...
3 - Квыводковым птицам относятся а) серая куропатка б) большая синица в) трёхпалый дятел...
1 - Вмагазине листы фанеры одинаковой толщины.у какого производителя цена за 1 квадратный...
2 - Как и почему звали коня македонского? как удалось ему его приручить? !...
2 - Решить уравнение x^2*2^(2sqrt(6-x))+4^(2-x)=16*4^(sqrt(6-x))+x^2*2^(-2x)...
1 - (1)жил у нас в доме огромный толстый кот – иваныч. (2)мы все его любили за добрый...
2 - Меня захватила эта книга потому что до сих пор я не знал ничего про индейцев синтаксический...
3 - 3x-8x+x=-32. если решите буду просто я тупой: d...
1 - Купили 78 кг муки. истратили 4/6 запаса. сколько кг осталось...
2 - Выполнить синтаксический разбор предложения не говори обиняком,режь правду прямиком...
3
Пусть x - скорость нагнетания воды первым насосом, пусть y - скорость нагнетания воды вторым насосом, пусть t - время. V - объём бассейна.
(x+y)*t=V; t=48/60=0,8.
xt1=y(t1+1/3)=(x+y)4/5;=> xt1=yt1+y/3=4x/5+4y/5;
t1(x-y)=y/3; =>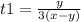
5xy=3(4x+4y)(x-y)=> 5xy=(4x+4y)(3x-3y)=>5xy=12(x*x-y*y)=> 12x*x-5xy-12y*y=0; (2)
(1)+(2):
24x*x-30xy=0 => 24x=30y=> 4xx=5y; => x=5y/4;
t1*5y/4=y(t1+1/3) => 5t1/4=t1+1/3 => 15t1=12t1+4 => 3t1=4 => t1=4/3
ответ: 4/3 часа