Два экскаватора, работая одновременно, могут вырыть котлован за 4ч 48 мин. если же сначала первый экскаватор выроет самостоятельно ¼ котлована, а затем второй – оставшуюся часть котлована ,то вся работа будет выполнена за 9 ч. за сколько часов может вырыть котлован каждый экскаватор, работая самостоятельно?

Ответы

karipzhanovalibek11 10.10.2020 02:23

Пусть х - производительность 1-го экскаватора; у - 2-го экскаватора; 1 - целый котлован.

Работая одновременно они выроют за 4 часов и ещё 48 минут:

$\frac{1}{x+y}$ = 4 $\frac{12}{15}$ = $\frac{72}{15}$

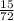
x + y = $\frac{15}{72}$

Второе уравнение, когда 1-й вырыл 1/4 котлована, а 2-й - 3/4 котлована:

$\frac{\frac{1}{4}}{x}$ + $\frac{\frac{3}{4}}{y}$ = 9

$\frac{1}{1x}$ + $\frac{3}{y}$ = 36

Из второго уравнения выражаем икс:

x =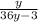 $\frac{y}{36y-3}$

И подставляем в первое уравнение:

$\frac{y}{36y-3}$ + y = $\frac{15}{72}$

Ну а дальше лень писать.

Короче просто делаешь квадратное уравнение из этого и считаешь отчеты через дискриминант. Удачи!

ПОКАЗАТЬ ОТВЕТЫ

angelina2334e35r5 21.01.2024 15:26

Давайте разберемся вместе.

Пусть первый экскаватор может вырыть котлован за х часов, а второй экскаватор может вырыть котлован за у часов.

Известно, что если два экскаватора работают одновременно, то они могут вырыть котлован за 4 часа 48 минут, что составляет 4 + 48/60 = 4.8 часов.

Запишем уравнение для работы двух экскаваторов:
1/х + 1/у = 1/4.8

Согласно условию задачи, первый экскаватор сначала вырыл 1/4 котлована, а затем второй экскаватор вырыл оставшуюся часть.

Запишем уравнение для работы экскаваторов по отдельности:
1/х + 1/у = 1/9

Теперь у нас есть два уравнения с двумя неизвестными (х и у). Решим их, чтобы найти значения х и у.

Составим систему уравнений:
1/х + 1/у = 1/4.8
1/х + 1/у = 1/9

Упростим уравнения, умножив оба уравнения на их общее кратное:
9/х + 9/у = 1
4.8/х + 4.8/у = 1

Из первого уравнения выразим 1/х:
1/х = 1 - 9/у
1/х = (у - 9)/у

Подставим это выражение во второе уравнение:
4.8/((у - 9)/у) + 4.8/у = 1

Упростим уравнение, умножив обе его части на у:
4.8y/(у - 9) + 4.8 = у

Разделим обе части уравнения на 4.8:
y/(у - 9) + 1 = у/4.8

Упростим уравнение:
y + у - 9 = у/4.8

Выразим у из этого уравнения:
у/4.8 - у = 9
у(1/4.8 - 1) = 9
у*0.8/4.8 = 9
у*0.1667 = 9
у = 9/0.1667
у ≈ 54

Теперь найдем х, подставив значение у в первое уравнение:
1/х + 1/54 = 1/4.8

Упростим уравнение, умножив обе его части на 4.8х:
4.8 + 4.8х/54 = х

Перенесем все слагаемые с х на одну сторону уравнения:
4.8х/54 - х = -4.8

Сделаем общий знаменатель в выражении слева:
4.8х - 54х/54 = -4.8

Упростим выражение:
(4.8х - 54х)/54 = -4.8

Сократим дробь на (4.8 - 54):
х(4.8 - 54) = -4.8 * 54

Раскроем скобки:
-49.2х = -259.2

Разделим обе части уравнения на -49.2:
х = -259.2/-49.2
х ≈ 5.267

Таким образом, первый экскаватор может вырыть котлован самостоятельно за примерно 5.267 часов, а второй экскаватор может вырыть котлован самостоятельно за примерно 54 часа.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра