Два автобуса вышли одновременно из пункта а в пункт в, расстояние между которыми 48км. скорость первого автобуса была на 4 км/ч больше, и поэтому он прибыл в пункт в на 10минут раньше. найдите скорость второго автобуса
Ответы
10 минут = 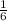 часа Пусть скорость второго автобуса равна х км/ч, тогда второго - (х+4) км/ч Составим уравнение:
часа Пусть скорость второго автобуса равна х км/ч, тогда второго - (х+4) км/ч Составим уравнение: 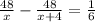 .
. 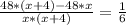 .
. 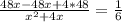 . Перекрёстным умножением:
. Перекрёстным умножением: 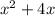 = 4*48*6
= 4*48*6 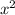 + 4x - 1152 = 0 x₁ =
+ 4x - 1152 = 0 x₁ = 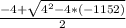 =
= 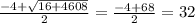 x₂ =
x₂ = 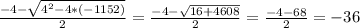 Скорость автобуса не может быть отрицательной, а значит, ответ задачи - x₁ ответ: скорость второго автобуса равна 32 км/ч
Скорость автобуса не может быть отрицательной, а значит, ответ задачи - x₁ ответ: скорость второго автобуса равна 32 км/ч
ПОКАЗАТЬ ОТВЕТЫ
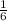 часа Пусть скорость второго автобуса равна х км/ч, тогда второго - (х+4) км/ч Составим уравнение:
часа Пусть скорость второго автобуса равна х км/ч, тогда второго - (х+4) км/ч Составим уравнение: 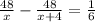 .
. 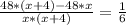 .
. 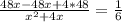 . Перекрёстным умножением:
. Перекрёстным умножением: 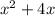 = 4*48*6
= 4*48*6 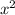 + 4x - 1152 = 0 x₁ =
+ 4x - 1152 = 0 x₁ = 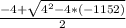 =
= 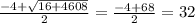 x₂ =
x₂ = 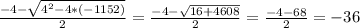 Скорость автобуса не может быть отрицательной, а значит, ответ задачи - x₁ ответ: скорость второго автобуса равна 32 км/ч
Скорость автобуса не может быть отрицательной, а значит, ответ задачи - x₁ ответ: скорость второго автобуса равна 32 км/ч
Другие вопросы по теме Алгебра
Популярные вопросы
- Вквадрате abcd с периметром равным 24 см проведена диагональ bd . чему равна...
3 - Валюмінієвий калориметр масою 50г,який містить 250 г води за температури 10градусів,впустили...
3 - Традиционная тематика бесед у и других народов...
3 - Исправить ошибки в программе#include #include #include #define _use_math_defines...
2 - Слогическими ,вообще не понимаю желательно с объяснением,а именно не понимаю...
1 - 4тапсырма мәтінге сүйеніп, сызбаны толтыр.күз мезгілі туралы әңгімеле....
3 - Легковой автомобиль массой 35 кг перемещается по горизонтали плоскости под действием...
3 - За які моральні якості сім богатирів полюбили царівну? 5 речень...
1 - Напишите аннотацию на тему бостандығы...
2 - Чи мають спільну точку прямі a i b, якщо при перетині їх січною c утворюються...
1