1. Алгебра
  2. Друзья решить неравенство

Друзья решить неравенство a) (x-1)(x+3)(x-2)(x^2+1)< 0

Мозг66615 Мозг66615    2   14.04.2019 14:42    2

Ответы
пушинка10 пушинка10  29.05.2020 11:26

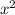(x-1)(x+3)(x-2)(x^{2}+1)<0

Рассмотрим все возможные случаи

\left \{ {{ (x-1)(x+3)(x-2)<0} \atop {x^{2}+10 }} \right.

\left \{ {{ (x-1)(x+3)(x-2)0} \atop {x^{2}+1<0 }} \right.

\left \{ {{x∈(-∞;-3)∪(1;2)} \atop {x∈R}} \right.

\left \{ {{x∈(-3;1)∪(2;+∞)} \atop {x∈∅}} \right.

затем найдем пересечение

в 1 случае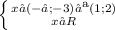 \left \{ {{x∈(-∞;-3)∪(1;2)} \atop {x∈R}} \right.

это х∈(-∞;-3)∪(1;2)

а во 2 случае

х∈∅

Находим объединение

это х∈(-∞;-3)∪(1;2)

Объяснение:

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
owlllllll owlllllll  27.10.2020 07:20
Дайте названия процессвязанных с движением литосферных плит 1) 2) 3) [3] b) Coo Соотнесите на границах между какими литосферными плитами мы можем наблюдать, процессы определенные...
nikiraspru nikiraspru  27.10.2020 07:20
11 августа 1804г что произошло в истории​...
victoriabetenecova victoriabetenecova  27.10.2020 07:20
6. Во сколько раз увеличится периметр квадрата,увеличилась в 16 раз?скор​...
ник5044 ник5044  27.10.2020 07:20
Из девяти узоров различных видов составляется мозаика из 5 их видов. Сколько можно составить различных мозаик?...
Полинаhelpme1 Полинаhelpme1  27.10.2020 07:20
Записать числа 250 и 0 025 в стандартном виде...
AlexBennet AlexBennet  27.10.2020 07:20
Составьте сложную функцию если f(x)=x3 , g(x)=3x+5,h(x)=cos x...
denic9 denic9  27.10.2020 07:20
8. Дана функция у = √x . a) График функции проходит через точку с координатами А (а.; 9). Найдите значение а. б) Если x ∈ [0;9], то какие значения будет принимать данная функция?...
malaya108 malaya108  10.09.2020 22:49
0,210010 округлите до 0,1 десятых...
шогвшвгвшр шогвшвгвшр  10.09.2020 22:49
Найдите значение выражения x^3+8y^3 если x+2y=3 xy=2очень нужно​...
George6666666 George6666666  10.09.2020 22:48
Раскройте скобки и приведите подобные слагаемые 7y-2(3y+8)​...

Популярные вопросы