1. Алгебра
  2. доведи,що функция у=х2(это

доведи,що функция у=х2(это в квадрате) + 8х+18 не може набувати вид'емних значень


доведи,що функция у=х2(это в квадрате) + 8х+18 не може набувати вид'емних значень

Вика1609000 Вика1609000    3   04.09.2020 02:27    1

Ответы
g1122611 g1122611  15.10.2020 17:21

Объяснение:

1) Коефіцієнт при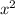 x^2 a=1, значить вітки графіка функції напрямлені вгору

Дискримінант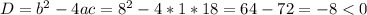 D=b^2-4ac=8^2-4*1*18=64-72=-8 - а значить перетину з віссю абсцис немає

графік функції лежить вище осі абсцис

=> дана функція не може приймати відємних значень

2) Коефіцієнт при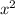 x^2 a=1, значить вітки графіка функції напрямлені вгору, і значить вершина параболи - точка абсолютного мінімуму значень функції.

x_W=\frac{-b}{2a}; y_W=c-\frac{b^2}{4a}

y_W=18-\frac{8^2}{4*1}=18-16=2 - найменше значення функції дорівнює 2, а значить

=> дана функція не може приймати відємних значень

3) Так як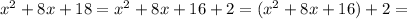 x^2+8x+18=x^2+8x+16+2=(x^2+8x+16)+2=

(x^2+2*4^x+4^2)+2=(x+4)^2+20

як сума невідємного виразу (квадрат будьякого виразу невідємна величина) і додатнього 2>0

=> дана функція не може приймати відємних значень


доведи,що функция у=х2(это в квадрате) + 8х+18 не може набувати вид'емних значень
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Кентервильский1монах Кентервильский1монах  19.03.2019 07:40
Cos 7x cos 3 x - sin 3 x sin 7 x - 1\2...
Tiktak222 Tiktak222  19.03.2019 07:40
Вравнобедренном треугольнике abc с основанием ac длина боковой стороны равна 20.найдите косинус угла bac если высота проведенная к основанию равна 12...
BelkaNext BelkaNext  19.03.2019 07:40
8! кто может ! вынесите множитель из-под знака корня. кводратный корень- к(так как значок я ствить не умею, заменяю буквой) /-дробь а теперь сами числа: к m(в третий степени)/n(в...
юра416 юра416  19.03.2019 07:40
Найдите общий множитель: 8х^6y^3-12x^3y^3...
alyakolomoets alyakolomoets  19.03.2019 07:40
16*(9 в степени х)-25*(12 в степени х)+9*(16 в степени х)=0...
ггвв ггвв  19.03.2019 07:40
X- 4/x - 2корня из x сократите дробь...
Лина7839 Лина7839  19.03.2019 07:40
Втреугольнике abc угол с равен 90, угол в равен 30, bc = 3 корень из 3. найдите ас...
pragravra pragravra  19.03.2019 07:40
1)2x+ac+cx+2a 2)2x+7y+14+xy 3)ay-12bx+3ax-4by...
garvarrd garvarrd  19.03.2019 07:40
№1. 4 х в квадрате - 36 х +77 = 0 №2. 15 у в квадрате - 22у - 37 = 0 №3. 7z в квадрате - 20 z +14 = 0 №4. у в квадрате - 10 у - 25 = 0...
chibitkova237 chibitkova237  13.09.2020 14:48
A1=5 An+1=2-an Найти:а2,а5,а4-?...

Популярные вопросы