Доведіть тотожність / докажите тотожность
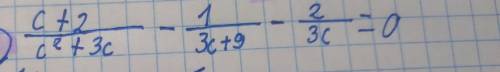
Другие вопросы по теме Алгебра
Популярные вопросы
- Задание 4 Подумай, какими качествами должен обладать человек, чтобы принести пользу...
2 - Меч работы гномов стоил 80 золотых. При покупке 8 таких мечей со скидкой 5% люди...
3 - 9. Установіть відповідність. Герої твору1 Бочонок, Зульфат2 Павлусь, наймичка3...
2 - Вкажіть сполуки при взаемодiї яких утворюються кислотні оксиди: А метал та кисень;...
2 - ЗАДАЧУ ПРИКРІПИЛА!сила тяжіння закон всесвітнього тяжіння...
1 - Рока л Read the text and choose the right variantRead the text and choose the right...
2 - Назывные предложения 1. Укажите односоставное предложение: а) Предрассветный туман....
3 - Вычислить площадь плоской фигуры с определённого интеграла y=0,5x^2-4x+10 y=x+2...
3 - 2. Вставьте необходимую степень сравнения и переведите: 1) The sound grew (faint)...
3 - Переказ У поли нужно очень ...
2
Объяснение:
Нужно доказать, что правая и левая части тождества равны.
Рассмотрим левую часть тождества:
Общий знаменатель :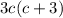
Первую дробь умножаем на 3, вторую на , третью на
, третью на 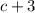 .
.
То есть левая часть тождества равна правой. Тождество доказано.