1. Алгебра
  2. Доведіть, що для будь-яких

Доведіть, що для будь-яких додатних чисел а,b і с виконується нерівність аb(а + b -2 с ) + bс(b+ с- 2а) + ас(а + с-2b) > 0

MrLegolas MrLegolas    3   27.05.2020 18:28    3

Ответы
Jand9 Jand9  15.10.2020 10:13

ab(a+b-2c)+bc(b+c-2a)+ac(a+c-2b)=a^2b+ab^2-2abc+b^2c+bc^2-2abc+a^2c+ac^2-2abc=(a^2b+bc^2)+(ab^2+b^2c)+a^2c+ac^2-6abc=b(a^2+c^2)+b^2(a+c)+ac(a+c)-6abc=b((a+c)^2-2ac)+(a+c)(b^2+ac)-6abc=b(a+c)^2-2ac+(a+c)(b^2+ac)-6abc=(a+c)(ab+bc+b^2+ac)-8abc=(a+c)(b(b+c)+a(b+c))-8abc=(a+c)(b+c)(a+b)-8abc.

Используем неравенство Коши о средних:

\frac{a+b}{2}\geq \sqrt{ab}\Leftrightarrow a+b\geq 2\sqrt{ab}\\\\\frac{a+c}{2}\geq \sqrt{ac}\Leftrightarrow a+c\geq 2\sqrt{ac}\\\\\frac{b+c}{2}\geq \sqrt{bc}\Leftrightarrow b+c\geq 2\sqrt{ac}

Перемножив все три неравенства, получаем, что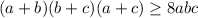 (a+b)(b+c)(a+c)\geq 8abc, причем для положительных чисел равенство возможно только в случае 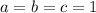a=b=c=1 (действительно: (1+1)(1+1)(1+1) ≥ 8 · 1 · 1 · 1 - верно). Неравенство доказано.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Hahaha1234567890 Hahaha1234567890  14.04.2020 18:55
Задание 1. Найдите А ∩ В, если а) А = (–2; 6), В = (1; 7); б) А = [0; 4], B = [4; 8]; в) А = (–∞; +∞), В = (–3; 9);...
YTTeamGardnYT YTTeamGardnYT  14.04.2020 18:55
РЕШИТЕ МОЖЕТЕ РАСПИСАТЬ ВСЕ НА ЛИСТЕ...
Гововрв Гововрв  14.04.2020 18:54
Выберите правильный ответ. В прямоугольном треугольнике АВС угол - прямой, угол А равен 64°, АB=20 см. Найдите ВС.​...
kruglov428 kruglov428  14.04.2020 18:54
Нужно решить уравнение 7 класс 625×(18)в квадрате×3в3степени×150разделить дробью5в квадрате×3в шестой степени×2во2степени=...
Toprangdheb Toprangdheb  14.04.2020 18:54
Дана функция y=a+4. При каких значениях a значение функции равно 4?​...
NancyKorea NancyKorea  14.04.2020 18:54
Реши уравнение: 4+4⋅(3⋅x+2)=6−5⋅x.(При необходимости, ответ округли до тысячных...
anyutra anyutra  14.04.2020 18:54
Знайдіть проміжки зростання і спадання функції y=0.2x ^5-x^3+2x-9...
leonik9797 leonik9797  14.04.2020 18:54
Построить график функции y=6x-4.Использую построенный график,ответить на во а)при каком значении x значение функции равно нулю ? б)при каком значении x значение равно 8 ? в) какое...
8007F300среднячок 8007F300среднячок  13.07.2019 14:40
Найдите значение выражения 23a-7b+2c при a=0.2, b=-5.4,c=-6.2...
Neznakomka111111 Neznakomka111111  13.07.2019 14:40
При каких m значениях 5x2+mx+20+12=0 имеет два корня?...

Популярные вопросы