Дорогу длиной 28км разделили на 3 неравные части. расстояние между серединами крайних частей равно 16км. найти длину средней части

Question

Алгебра: Дорогу длиной 28км разделили на 3 неравные части. расстояние между серединами крайних частей равно 16км. найти длину средней части

osadchevasasha · Answer

Пусть наш путь - это сумма длин 3 неравных частей. Пусть это будут части с длинами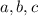 a,b,c

Известно, что общая длина равна 28 км. То есть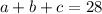 a+b+c=28

Крайние части - части с длинами , .

Середина делит часть пополам. А расстояние между серединами крайних частей затрагивает одну половину от , одну половину от и всю .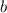

Тогда получаем, что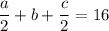 $$\frac{a}{2}+b+\frac{c}{2}=16$ км.

Из этого получается система:

$$\left \{ {{a+b+c=28} \atop {\frac{a}{2}+b+\frac{c}{2}=16 }} \right.$

Вычтем из первого уравнения системы второе, тем самым исключив b.

Получаем:

$$a+b+c-(\frac{a}{2}+b+\frac{c}{2})=28-16; a-\frac{a}{2}+b-b+c-\frac{c}{2}=12; \frac{a}{2}+\frac{c}{2}=12$

То есть a+c=24

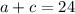
Мы знаем, что

$a+b+c=28; a+c=28-b \Rightarrow 24=28-b \Rightarrow b=4$ (км)

ответ: длина средней части дороги равна 4 км.