1. Алгебра
  2. Докажите тождество хотя бы с 1

Докажите тождество хотя бы с 1 из 2


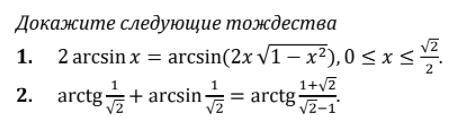
Докажите тождество хотя бы с 1 из 2

катя19052 катя19052    2   16.09.2021 03:16    0

Ответы
lizaaf lizaaf  16.09.2021 06:00

Объяснение:

\small2 \arcsin{x} = \arcsin(2x \sqrt{1 - {x}^{2} } ); \: 0 \leqslant x \leqslant \frac{ \sqrt{2} }{2}

Рассмотрим по отдельности правую и левую часть тождества.

Т к имеются ограничения на значение х, для удобства можно произвести замену переменной:

x = \sin{y} ; \\

ограничив соответственно значение у пределами, такими что:

0 \leqslant y \leqslant \tfrac{\pi}{4} < = \sin{0} \leqslant \sin{y}{ =} x \leqslant \sin \tfrac{\pi}{4} \\ 0 \leqslant x \leqslant \tfrac{ \sqrt{2} }{2} \:

После замены получаем следующее выражение. В левой части будет:

\small2 \arcsin{( \sin{y}) } = 2y; \: 0 \leqslant y \leqslant \tfrac{\pi}{4} ;

В правой части:

\arcsin(2x \sqrt{1 - {x}^{2} } ) = \\ = \arcsin \big(2 \sin{y} \sqrt{1 - \sin {}^{2}y } \big)

так как для

\forall{y} \in [0;\tfrac{\pi}{4}]\: \sin{y} \geqslant 0; \: \cos{y} \geqslant 0

то можем преобразоватт выражение в правой части следующим образом:

\arcsin(2x \sqrt{1 - {x}^{2} } ) = \\ = \arcsin \big(2 \sin{y} \sqrt{1 - \sin {}^{2}y } \big) = \\= \arcsin \big(2 \sin{y} \sqrt{ \cos {}^{2}y } \big) = \\ = \arcsin \big(2 \sin{y} \: \cos {y} \big) = \\ = \arcsin( \sin{2y}) =2y; \: 0 \leqslant y \leqslant \frac{ \pi}{4}

В результате, как мы видим, и в правой и в левой части мы получили одно и то же выражение. Следовательно, тождество верно

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
uylia144348 uylia144348  17.08.2019 04:30
Решить логарифмическое уравнение: а) log1/7(4+1)=-2 б) lg(3-x)-lg(x+2)=2lg_2 в)x^(lgx-2)=1000...
3333231231 3333231231  17.08.2019 04:30
Баржа по течению 56 км и, повернув обратно еще 42 км, затратив на весь путь 7 часов. найдите собственную скорость баржи если скорость реки равна 5 км/ч....
Еее11111111 Еее11111111  17.08.2019 04:30
Решить уравнение 6,3+7,8j-3,6j=j-12,9-7,3j...
gzemdihanova gzemdihanova  17.08.2019 04:30
Среди чисел 4√3-7,-4√3-7,1/4√3+7 найдите пару взаимно обратных чисел...
artemafanasev2003 artemafanasev2003  17.08.2019 04:30
Решить 1)(3а-1)^2 (ну тоесть в квадрате) 2)(5x+8y)(8y-5x) 3)(11+4k)^2 (в квадрате) 4)(2с-1)^2 ( в квадрате) 5)(9+3x)^2 (в квадрате)...
Raimbek711 Raimbek711  17.08.2019 04:30
Впрямоугольнике abcd ab=15 см ,ac=17см . найдите плошадь прямоугольник...
slavuka slavuka  17.08.2019 04:30
Найдите значение выражения (3 корень 5) в квадрате (в числителе), 15 в знаменателе...
ната5810 ната5810  05.08.2019 07:10
Найти общий вид первообразной.: f(x)=11+1/x^2+x^5...
KatyaKuxar KatyaKuxar  05.08.2019 07:10
1.решите уравнение: а)5х-17=13-х; б)4х-9(х-7)=-12; в)0,4(3х+1)=5,6-3(2-0,4х) 2. при каком значении переменной у, значение выражения 3у-11 в три раза меньше значения выражения 5у-17?...
КилоЛеденцов КилоЛеденцов  05.08.2019 07:10
Найдите крень уравнения 5=-0,2икс-5...

Популярные вопросы