Докажите тождество: 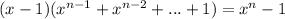
где n натуральное число больше1
Другие вопросы по теме Алгебра
Популярные вопросы
- Оқиық және жауап берейік 5. Сұрақтарға жауап бер. Суреттен тауып көрсет.Тілеуханның...
3 - Ти пізда піздатая, я відсосу тобі в очко!...
2 - Переведите Sunday 27th December Hi Molly, Greetings from Australia!...
2 - Диктант. Списати, поставити пропущені розділові знаки (розділові знаки,...
2 - У чому алегорія оповідання Г. Пагутяк «Потрапити в сад»?...
1 - Поставте дієслова в усіх особових формах однини і множини. Терпіти-...
3 - Напиши сочинение на тему «Какой необычный и радостный подарок я бы...
2 - 2. ... Volga is ... longest river in ... European part of ... Russia....
1 - Длина светогово дня южном и северном можно по быстрее ...
1 - 4-тапсырма, 129-бет. Мәтінді оқып, мәтінге 5 сұрақ құрастыр. Прочтите...
1
Раскроем скобки:
Заметим, что все слагаемые, кроме первого и последнего взаимно уничтожаются: