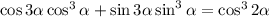Докажите тождество cos 3α*cos ^3α+sin 3α*sin^(3)α=cos 2α
Другие вопросы по теме Алгебра
Популярные вопросы
- НАйти координаты вектора х...
3 - Скажите название автора от куда взята эта контрольная?...
1 - 9. Первым фараоном Египта был... Хаммурапи Татуанхамон Рамсес...
3 - Сколько энергии приобретёт при плавнении кусок свинца массой...
2 - який рівень організації живого вивчає цитологія та гістологія...
3 - Ребят подскажите сколько на 4 уровне клеточек?...
1 - Как затраты на военные нужды влияли на развитие НТП в странах...
1 - Какое количество кислорода в 8 граммах...
2 - На бумажке электронными цифрами напечатано число 56789. Как разрезать...
2 - НЕИ ИЗ ИНТЕРНЕТА Я ТАМ ВСЁ ВИДЕЛ Раскройте смысл фрагмента текста...
3
Нужно доказать