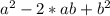Докажите справедливость равенства 1) (-a - b)^2=(a+b)^2 2) (-a + b)^2 = ( b - a )^2 3) (-a + b)^2 = (-b + a)^2 ^-степень. заранее большое
Другие вопросы по теме Алгебра
Популярные вопросы
- 1. Наливаем в пробирку раствор купрум (II) сульфата объемом 1 мл и добавляем...
3 - У піраміди площа основи дорівнює 3см, а площа бічної поверхні 5см, знайдіть...
2 - Схарактеризуйте поезію В. Стуса «Ярій душе»....
2 - с задачей по экономической статистики. Имеются следующие данные об элементах...
3 - В основі піраміди лежить ромб, сторона якого 5 см, а висота 1см, знайдіть...
3 - 1)для распространения с воды семенам необходимо иметь .а) острые зубчики б)...
1 - Арены. Бензол как представитель аренов. Гомологи бензола, из номенклатура,...
2 - Сакские племена (хаомаварга, тиграхауда, парадарайя, аримаспа и др.) - экономические,...
2 - найти трэк клип начинается с того что парень приходит домой и его встречает...
2 - Функция y=f(x) определена на промежутке (-6;6) Напишите 1)D(y) 2)E(y) 3)корни...
1
1)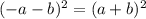
(-a-b)*(-a-b)= [-(a+b)]*[-(a+b)]= (-1)*-(1)*(a+b)*(a+b)=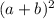
или (-a-b)*(-a-b)=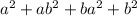 =
=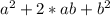
(a+b)*(a+b)=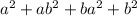 =
=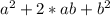
2)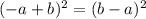
От перестановки мест слагаемых алгебраическая сумма не меняется, поэтому
(-a+b)=b-a
3)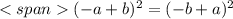
(-a+b)* (-a+b)=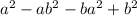 =
=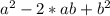
(-b + a)*(-b + a)=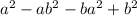 =
=