Докажите методом математической индукции:
2)7^n +3n -1 кратно 9

Ответы

ksyu5551 25.12.2020 06:32

$(7^n +3n -1)\ \vdots\ 9$

1 шаг. Проверим справедливость утверждения при n=1:

$7^1+3\cdot1-1=7+3-1=9\ \vdots\ 9$ - верно

2 шаг. Предположим, что при n=k следующее утверждение верно:

$(7^k +3k -1)\ \vdots\ 9$

3 шаг. Докажем, что при n=k+1 следующее утверждение также будет верно:

$(7^{k+1} +3(k+1) -1)\ \vdots\ 9$

Для доказательства выполним преобразования:

$7^{k+1} +3(k+1) -1=7\cdot7^k+3k+3-1=7^k+6\cdot7^k+3k+3-1=$

$=(7^k+3k-1)+6\cdot7^k+3=(7^k+3k-1)+3(2\cdot7^k+1)$

Рассмотрим получавшуюся сумму. Первое слагаемое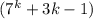 (7^k+3k-1) делится на 9 по предположению, сделанному на предыдущем шаге. Во втором слагаемом 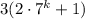$3(2\cdot7^k+1)$ первый множитель делится на 3. Значит, остается доказать, что второй множитель также делится на 3. Докажем это, используя арифметику остатков:

$2\cdot7^k+1\equiv2\cdot(7-2\cdot3)^k+1=2\cdot1^k+1=2\cdot1+1=2+1=3\pmod{3}$

Мы получили, что выражение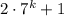 $2\cdot7^k+1$ дает при делении на 3 такой остаток, как и число 3. Но число 3 кратно 3, значит и выражение 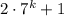$2\cdot7^k+1$ кратно 3.

Возвращаясь к выражению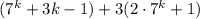 $(7^k+3k-1)+3(2\cdot7^k+1)$ , повторим, что первое слагаемое делится на 9, второе слагаемое представляет собой произведение двух множителей, каждое из которых делится на 3, то есть само слагаемое делится на 9. Сумма двух выражений, делящихся на 9, также делится на 9, или другими словами, кратна 9. Доказано.