Докажите, используя принцип математической индукции, что для любого натурального числа n верно равенство: Решите
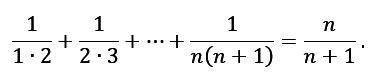
Другие вопросы по теме Алгебра
Популярные вопросы
- Дорогие , что означает этот знак ^? его пишут в примеры, но что оно означает?...
3 - Естественный прирост населения небольшого поселка составил 17 человек на...
1 - Переставить и составить предложение was/hair/your/what/like?...
3 - Создайте таблицу истинности для каждого из следующих предложений. а. если...
2 - Тогда и я на дерево полез собрал грибы и принёс к берете подчеркнуть однородные...
2 - Найдите сумму первых десяти членов арифметической прогрессии,если а1=10,а10=-22....
2 - Какой потенциальной относительностью земли обладает тело массой 100 килограммов...
3 - Занятия дворян во второй половине 19 века?...
1 - Висят грибные шляпки на сучках дерева синтаксический разбор простого предложения...
1 - Срешением. алкан с относительной молекулярной массой 58, — это а этан. б...
1
Чтобы доказать это равенство, мы воспользуемся принципом математической индукции. Принцип математической индукции используется для доказательства утверждений, которые зависят от натурального числа n.
Шаг 1: База индукции
В базе индукции мы проверяем, выполняется ли равенство для наименьшего значения n, то есть n = 1.
Подставим n = 1 в данное равенство:
(1^2 + 2^2 + 3^2 + ... + 1^2 + n^2) = (n*(n+1)*(2n+1))/6
(1^2) = (1*(1+1)*(2*1+1))/6
1 = (1*2*3)/6
1 = 6/6
1 = 1
Таким образом, равенство выполняется при n = 1.
Шаг 2: Предположение индукции
Мы предполагаем, что равенство выполняется для некоторого числа k, то есть предполагаем, что (1^2 + 2^2 + 3^2 + ... + 1^2 + k^2) = (k*(k+1)*(2k+1))/6.
Шаг 3: Индукционный переход
Мы должны доказать, что если равенство выполняется для числа k, то оно также выполняется для k + 1.
Подставим n = k + 1 в данное равенство:
(1^2 + 2^2 + 3^2 + ... + 1^2 + k^2 + (k + 1)^2) = (k + 1)*((k + 1) + 1)*(2(k + 1) + 1))/6
(1^2 + 2^2 + 3^2 + ... + 1^2 + k^2 + (k + 1)^2) = (k + 1)*(k + 2)*(2k + 3))/6
Мы можем заметить, что левая часть равенства (1^2 + 2^2 + 3^2 + ... + 1^2 + k^2 + (k + 1)^2) соответствует сумме первых (k + 1) квадратов, а правая часть равенства ((k + 1)*(k + 2)*(2k + 3))/6 соответствует формуле для суммы первых (k + 1) квадратов.
По нашему предположению индукции, левая часть равенства равна ((k*(k+1)*(2k+1))/6 + (k + 1)^2) = ((k*(k+1)*(2k+1) + 6(k + 1)^2))/6.
Теперь мы можем преобразовать это равенство:
((k*(k+1)*(2k+1) + 6(k + 1)^2))/6 = ((k + 1)*((k*(2k+1))/6 + 6(k + 1)))/6 = ((k + 1)*((k*(2k+1) + 36(k + 1)))/6.
Таким образом, мы получаем: ((k + 1)*((k*(2k+1) + 36(k + 1)))/6 = (k + 1)*(k + 2)*(2k + 3))/6.
Таким образом, равенство выполняется для n = k + 1.
Шаг 4: Заключение
Мы доказали, что используя принцип математической индукции, для любого натурального числа n выполняется равенство (1^2 + 2^2 + 3^2 + ... + 1^2 + n^2) = (n*(n+1)*(2n+1))/6.
Я надеюсь, что данное объяснение помогло вам понять решение данной задачи! Если у вас остались вопросы, пожалуйста, не стесняйтесь задавать их.