Докажите, что значение выражения
)
не зависит от значения переменной.
Другие вопросы по теме Алгебра
Популярные вопросы
- Гора-горный.лиса -леса.осина-осиновый.являются ли однокоренными пары слов...
3 - что будет если все бактерии исчезнут с лица земли эссе биология на страницу...
2 - Где главные и второстепенные члены в предложении. папа выглядел в своем новом...
3 - 15 предложений на тнму тире между подлежащими и сказуемыми...
1 - Прочитайте докажите что данное предложение сложное выделенные слова омонимы...
1 - Запиши как называется разряд в котором стоит цифра 2,5,1...
1 - Примеры рек экваториального ,субэкваториального и тропического поясов на...
1 - Назовите главную причину сокращения видового состава цветковых растений 1.деятельность...
1 - Какую социальную общность выделяют по этническому признаку: 1-православие...
2 - 99 ! нужно составить рассказ от имени горожанина в средние века о + и - проживании...
3
ответ: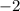 .
.
Объяснение:
ответ: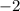 .
.