Докажите, что является чётной функция у = f(x) 1)
2)
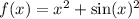
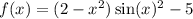
Другие вопросы по теме Алгебра
Популярные вопросы
- Вдвух хранилищах было 760т овощей .когда из первого хранилища увезли 180т...
3 - Какие вы знаете календарно обрядовые песни...
1 - Виразити у кілометрах за годину 2 м/c , 5 м/c , 8 м/c , 50 м/c , 100 м/c...
2 - Решить? запиши подряд как одно число.назови получившиеся числа.(а).цифры...
1 - Решить для приготовления каши бабушка из килограммового пакета крупы трижды...
3 - Решите первое рыболовецкое судно выловило 18 970 кг рыбы это на 8370 кг...
1 - Какие ответы на вопрос о единстве всемирной вам известны? какой подход...
1 - Рассчитайте массу одной молекулы нитрата натрия....
3 - Вкружках народного творчества занимается 84 учащихся.одна третья часть...
1 - Как записать число 437, 105 ; 92,352; 0,00000085 и0,000079 в стандартном...
3
Докажите четность функции.
Объяснение:
1.
==>
==>
==>
Функция четная.
2.
==>
==>
==>
Функция четная.