докажите, что произведение двух последовательных натуральных чисел, кратных трем, будет четным числом
Другие вопросы по теме Алгебра
Популярные вопросы
- (х – 7) (+1) (1 — 3) 0)теңсіздікті шешіңдер!помагите...
3 - Составь расказ об археогическом памятнике сармтов филипповском курган по плану:...
2 - Опишите биологические значения митоза и мейоза в жизнедеятельности живых организмах...
2 - Сульфиды - это биэлементные соединения, в состав которыхобязательно входит сера(...
2 - Решите неравентсва, используя метод интервалов...
3 - 1. Вычисли объем куба с ребром a, равным 20 см. 2. Вычисли объем параллелепипеда,...
2 - ОЧЕНЬ а)основные статьи экспорта и импорта Амурской областиб)что, кроме сырья,...
3 - Музыка в нашей жизни, музыка Объединвшихся поколения...
2 - Жил был в деревянный дом имена существительные найти...
1 - написать эссе на тему:Роль Абая в истории Казахстана ребята...
3
Пусть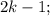
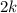 два последовательных натуральных числа, тогда
два последовательных натуральных числа, тогда
Найдём их произведение:
В полученном произведении один из множителей делится на 2, значит, и всё произведение делится на 2, т.е. это будет четное число.
Доказано.