Докажите, что при любом натуральном n число n^3+3n^2+6n+8 является составным

Ответы

Пеперони228 23.05.2020 22:46

$\displatstyle n\in \mathbb{N} \Rightarrow (n^3 +3n^2 +6n+8)\in \mathbb{N}$ т.к. произведение и сумма натуральных чисел равны натуральному числу.

Натуральное число ОБЯЗАТЕЛЬНО, либо составное, либо простое.

$\displatstyle n^3 +3n^2 +6n+8=\\=(n^3 +2^3)+(3n^2 +6n)=\\=(n+2)(n^2 -2n+4)+3n(n+2)=\\=(n+2)(n^2 -2n+4+3n)=\\=(n+2)(n^2 +n+4)$

Любое простое число можно представить как произведение 1 и самого себя. Если выражение это простое число, то хотя бы один из множителей равен 1.

(n+2) ≥ 3 при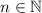 $\displatstyle n\in \mathbb{N}$

(n²+n+4) ≥ 6 при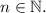 $\displatstyle n\in \mathbb{N} .$ Т.к. при минимальном n=1, выражение равно 6. А чем больше n, тем больше значение выражения.

Итог: ни один из множителей не может равняться 1, поэтому выражение не может быть простым числом. А значит оно составное.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

мишка2283 30.11.2020 21:00

Anastasiagoodnastia 30.11.2020 20:59

YTMrBreadYT 30.11.2020 20:59

ответы запишите в порядке убывания степеней...

Cerd 08.04.2021 12:31

хорошист540 08.04.2021 12:31

djsxv 08.04.2021 12:32

ЮляЯяя1111 08.04.2021 12:32

londi17 08.04.2021 12:32

Будь ласка знайдіть x0 до функції дотичної...

Давидычь 09.09.2019 09:40

netznanie 09.09.2019 09:40

Решите уровние: 1-2x/3 +2-3x/4+x/5=1/12 распишите подробно....