Докажите, что при a>0, b>0, c>0:
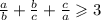
Другие вопросы по теме Алгебра
Популярные вопросы
- 25x^2 -10x+4=(sqrt3-cos(15πx/+cos(15πx/2))...
2 - Вычислите поразрядную конъюнкцию двоичных чисел 11110011 и 11001101. ответ...
1 - Как вы думаете все животные полезны какие животные приносят человеку вред...
2 - Отличаются ли врач от доктора, и чем если да?...
3 - План сказки слон на імя гудзик...
2 - Конкретная ситуация. фирма сатурн широко известная на отечественном и зарубежном...
1 - А1. что соединяет среднее ухо с глоткой? 1) барабанная перепонка 2) евстахиева...
3 - Что объединяет пьесу-сказку снегурочка и миф о деметре...
3 - Умоляю я не поняла тему все примеры все...
2 - 1)у всех африканских львов,обитающих в саванне,под глазами белые пятна....
2
(см. объяснение)
Объяснение:
Рассмотрим сумму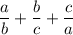 .
.
Из неравенства Коши имеем:
Доказано!