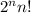Докажите,что (n+1)(n+2)...(2n-1)*2n/1*3*5*...*(2n-1)=2^n
Другие вопросы по теме Алгебра
Популярные вопросы
- 1. составьте предложения из следующих слов в соответствии с порядком слов...
3 - Впервом ящике имеются 12 белых и 6 черных шаров, а во втором 8 белых и 4...
2 - нам оценки за олимпиаду ставят...
2 - Заполните таблицу 2.4, если амортизация рассчитывалась линейным методом.таблица...
2 - Too and not enough 5 write pairs of sentences with too and (not) enough....
1 - Найдите формулу общего члена ряда 2+3/2+4/3...
1 - Найдите девятнадцатый член арифметической прогрессии: 7;...
1 - Сравни толщину нитей основные и уточные...
1 - Вычислите массу вещества, оставшегося в электролизе и количество вещества,...
2 - Напишите письмо петру владиславичу от имени солдата подвергнутого в жёсткой...
2
Ч.т.д.
_________
Свойство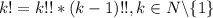 очевидно (k и k-1 - последовательные натуральные числа, а значит они имеют разную четность, а значит один из сомножителей содержит все четные числа, а 2ой - все нечетные из отрезка [1;k], т.е. их произведение содержит все натуральные числа отрезка [1;k] по одному разу. А это и есть
очевидно (k и k-1 - последовательные натуральные числа, а значит они имеют разную четность, а значит один из сомножителей содержит все четные числа, а 2ой - все нечетные из отрезка [1;k], т.е. их произведение содержит все натуральные числа отрезка [1;k] по одному разу. А это и есть 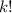 )
)
Пояснение к преобразованию![(2n)]() : в этом выражении содержится произведение всех четных чисел отрезка [1;2n] , всего этих сомножителей
: в этом выражении содержится произведение всех четных чисел отрезка [1;2n] , всего этих сомножителей 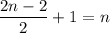 , причем k-ый из них представим в виде
, причем k-ый из них представим в виде 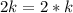 . А тогда, вынеся из каждого сомножителя 2, и получим представление
. А тогда, вынеся из каждого сомножителя 2, и получим представление