Докажите, что функция y=sin2x является возрастающей на множестве. За ответ заранее
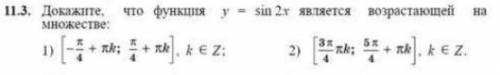
Другие вопросы по теме Алгебра
Популярные вопросы
- Определить вид изгиба в сечении 1-...
1 - Что вызывает изменение поверхности Земли? Отметьте только те процессы,...
2 - План к роману Остров Сокровищ из 3 пунктов....
3 - Что такое популяция? Группа свободно скрещивающихся между собой...
3 - Астындағы берілген сөздерге фонетикалық талдау жаса: Тәрбие басы-тіл(М.Қ.)...
1 - Мдк 01.01 сварка Сварка низколегированных молибденовых и хроммолибденовых...
1 - Read and complete: Were you and Sally at home last evening? No,...
1 - Цепь питания это.. несколько последовательных рядов организмов,...
3 - Заряд 20 нКл перемістився в електричному полі з точки, потенціал...
3 - Rewrite into reported sentences 1. When does the plane to Chicago...
1
Шаг 1: Найдем производную функции y = sin(2x).
Для этого воспользуемся правилом дифференцирования для синуса.
Производная синуса функции будет равна косинусу этой функции, умноженному на производную аргумента.
dy/dx = (cos(2x)) * (d(2x)/dx)
Производная аргумента d(2x)/dx равна 2.
Таким образом, производная функции y = sin(2x) будет равна:
dy/dx = (cos(2x)) * 2
Выражение (cos(2x)) * 2 можно упростить до 2*cos(2x).
Шаг 2: Анализ производной.
Если производная функции положительна на заданном множестве, то это означает, что функция возрастает на этом множестве.
Таким образом, нам нужно доказать, что 2*cos(2x) > 0 на заданном множестве.
Шаг 3: Выясним, когда выражение 2*cos(2x) > 0.
Откуда мы знаем, что cos(x) положителен при x ∈ [0, π] и x ∈ [2π, 3π], так как cos(x) является положительным на этих интервалах.
Таким образом, чтобы 2*cos(2x) было положительным, мы должны учитывать условия:
(1) cos(2x) > 0
(2) 2x ∈ [0, π] или 2x ∈ [2π, 3π] (чтобы включить значения x, при которых cos(2x) > 0)
Шаг 4: Вывод.
Таким образом, функция y = sin(2x) будет возрастающей на множестве x, таком что (2x ∈ [0, π]) или (2x ∈ [2π, 3π]), так как в этом случае 2*cos(2x) > 0, и производная положительна.
Итак, функция y = sin(2x) является возрастающей на указанном множестве x.