Докажите что функция f(x)=x^2-10x возрастает на промежутке [5; +бесконечности) (без подстановки! )

Question

Алгебра: Докажите что функция f(x)=x^2-10x возрастает на промежутке [5; +бесконечности) (без подстановки! )

drgotika2011 · Answer

Пусть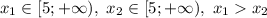 .Оба числа неотрицательны, поэтому при возведении в квадрат знак не меняется:На заданном промежутке большему значению аргумента соответствует большее значение функции, значит, функция возрастает, что и требовалось доказать....

Докажите что функция f(x)=x^2-10x возрастает на промежутке [5; +бесконечности) (без подстановки! )

Популярные вопросы