Докажите, что если x>0, y>0 и a>b, то 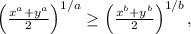
причем равенство возможно только при x=y.
Здесь a и b - любые действительные числа (с естественным ограничением 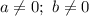 )
)
Ответы
Показать ответы (3)
Другие вопросы по теме Алгебра
Популярные вопросы
- Первый цех производит 15 деталий в час.второй производит за 8-часовой рабочий день...
1 - Решить 3 уровнения 7x+2=0,8x-4=0 ,4x+8=0....
3 - Особенности положения смешанных лесов...
3 - Некто пообещал дать 99 конфет тому, кто сумеет их разделить между четырьмя людьми...
3 - Сочинение на тему мои зимние каникулы!...
1 - Составь и запиши предложения,употребляя имена существительные в форме множественного...
2 - Морфологический разбор слова располагало) пример в предложении : и эта довольная...
2 - Представьте себе,что вам необходимо убедить своего товарища в том, что он должен...
2 - Образуй и запиши слова, обозначающие приказ (сказал- )...
2 - Что важнее - личные достинства человека или его происхождение в той или иной семье?...
2