Докажите, что если дробь а-в/а+в, где а и в - некоторые натуральные числа, причем а в, несократимые числа, то несократима также и дробь

Question

Алгебра: Докажите, что если дробь а-в/а+в, где а и в - некоторые натуральные числа, причем а в, несократимые числа, то несократима также и дробь а/в.

den4ik143 · Answer

Доказательство от противного:

Предположим, дробь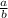 $\frac{a}{b}$ сократима. Это означает, что у чисел а и b есть общий простой множитель (назовем его k). Тогда число а можно представить в виде произведения mk, а число b - в виде произведения nk. Заменим а и b в дроби 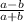$\frac{a-b}{a+b}$ на эти выражения, получим:

$\frac{mk-nk}{mk+nk}$ .

Вынесем k за скобки:

$\frac{k(m-n)}{k(m+n)}$

Числитель и знаменатель этой дроби можно сократить на k, но это противоречит условию, в котором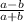 $\frac{a-b}{a+b}$ - несократимая дробь. Значит, наше предположение о том, что дробь 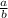$\frac{a}{b}$ сократима - неверно, т.е эта дробь является несократимой (что и требовалось доказать)

Докажите, что если дробь а-в/а+в, где а и в - некоторые натуральные числа, причем а> в, несократимые числа, то несократима также и дробь а/в.

Популярные вопросы