Докажите, что если a,b и y-углы треугольника,то верно равенство

Ответы

Иван55551 01.10.2020 07:23

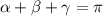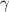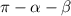Так как сумма углов в треугольнике равна $\alpha+\beta+\gamma=\pi$ , то вместо $\gamma$ запишем $\pi-\alpha-\beta$ .

Тогда

$\tan\frac{\alpha}{2}\tan\frac{\beta}{2}+\tan\frac{\beta}{2}\tan\frac{\pi-\alpha-\beta}{2}+\tan\frac{\pi-\alpha-\beta}{2}\tan\frac{\alpha}{2}\quad (*)$

Вычислим отдельно тангенс.

$\tan\frac{\pi-\alpha-\beta}{2}=\frac{\sin\frac{\pi-\alpha-\beta}{2}}{\cos\frac{\pi-\alpha-\beta}{2}}$

Вычислим отдельно числитель и знаменатель

Числитель равен

$\sin\frac{\pi-\alpha-\beta}{2}=\sin\left(\frac{\pi}{2}-\frac{\alpha+\beta}{2}\right)=\sin\frac{\pi}{2}\cos\frac{\alpha+\beta}{2}-\cos\frac{\pi}{2}\sin\frac{\alpha+\beta}{2}=$

$=1*\cos\frac{\alpha+\beta}{2}-0*\sin\frac{\alpha+\beta}{2}=\cos\frac{\alpha+\beta}{2}$

Знаменатель равен

$\cos\frac{\pi-\alpha-\beta}{2}=\cos\left(\frac{\pi}{2}-\frac{\alpha+\beta}{2}\right)=\cos\frac{\pi}{2}\cos\frac{\alpha+\beta}{2}+\sin\frac{\pi}{2}\sin\frac{\alpha+\beta}{2}=$

$=0*\cos\frac{\alpha+\beta}{2}+1*\sin\frac{\alpha+\beta}{2}=\sin\frac{\alpha+\beta}{2}$

Значит

$\tan\frac{\pi-\alpha-\beta}{2}=\frac{\cos\frac{\alpha+\beta}{2}}{\sin\frac{\alpha+\beta}{2}}=\cot\frac{\alpha+\beta}{2}$

Подставим в исходную формулу (*)

$\tan\frac{\alpha}{2}\tan\frac{\beta}{2}+\tan\frac{\beta}{2}\cot\frac{\alpha+\beta}{2}+\cot\frac{\alpha+\beta}{2}\tan\frac{\alpha}{2}=$

$=\tan\frac{\alpha}{2}\tan\frac{\beta}{2}+\cot\frac{\alpha+\beta}{2}*(\tan\frac{\beta}{2}+\tan\frac{\alpha}{2})=$

$\tan\frac{\alpha}{2}\tan\frac{\beta}{2}+\cot\frac{\alpha+\beta}{2}*\left(\frac{\sin\frac{\beta}{2}}{\cos\frac{\beta}{2}}+\frac{\sin\frac{\alpha}{2}}{\cos\frac{\alpha}{2}}\right)=$

$=\tan\frac{\alpha}{2}\tan\frac{\beta}{2}+\cot\frac{\alpha+\beta}{2}*\left(\frac{\sin\frac{\beta}{2}\cos\frac{\alpha}{2}}{\cos\frac{\alpha}{2}\cos\frac{\beta}{2}}+\frac{\sin\frac{\alpha}{2}\cos\frac{\beta}{2}}{\cos\frac{\alpha}{2}\cos\frac{\beta}{2}}\right)=$

$=\tan\frac{\alpha}{2}\tan\frac{\beta}{2}+\cot\frac{\alpha+\beta}{2}*\left(\frac{\sin\frac{\beta}{2}\cos\frac{\alpha}{2}+\sin\frac{\alpha}{2}\cos\frac{\beta}{2}}{\cos\frac{\alpha}{2}\cos\frac{\beta}{2}}\right)=$

По формуле синуса суммы

sin(x+y)=sinx*cosy+sinycosx

преобразуем числитель в скобках

$=\tan\frac{\alpha}{2}\tan\frac{\beta}{2}+\cot\frac{\alpha+\beta}{2}*\frac{\sin\frac{\alpha+\beta}{2}}{\cos\frac{\alpha}{2}\cos\frac{\beta}{2}}=$

Снова распишем котангенс по определению

$=\tan\frac{\alpha}{2}\tan\frac{\beta}{2}+\frac{\cos\frac{\alpha+\beta}{2}}{\sin\frac{\alpha+\beta}{2}}*\frac{\sin\frac{\alpha+\beta}{2}}{\cos\frac{\alpha}{2}\cos\frac{\beta}{2}}=$

Проведем сокращения

$=\tan\frac{\alpha}{2}\tan\frac{\beta}{2}+\frac{\cos\frac{\alpha+\beta}{2}}{\cos\frac{\alpha}{2}\cos\frac{\beta}{2}}=$

По формуле

$\tan x=\frac{\sin x}{\cos x}$ преобразуем выражение далее

$=\frac{\sin\frac{\alpha}{2}\sin\frac{\beta}{2}}{\cos\frac{\alpha}{2}\cos\frac{\beta}{2}}+\frac{\cos\frac{\alpha+\beta}{2}}{\cos\frac{\alpha}{2}\cos\frac{\beta}{2}}=\frac{\sin\frac{\alpha}{2}\sin\frac{\beta}{2}+\cos\frac{\alpha+\beta}{2}}{\cos\frac{\alpha}{2}\cos\frac{\beta}{2}}$

Распишем в числителе косинус суммы по формуле

cos(x+y)=cosxcosy-sinxsiny

После несложных преобразований и сокращения, получим нужное

$=\frac{\sin\frac{\alpha}{2}\sin\frac{\beta}{2}+\cos\frac{\alpha}{2}\cos\frac{\beta}{2}-\sin\frac{\alpha}{2}\sin\frac{\beta}{2}}{\cos\frac{\alpha}{2}\cos\frac{\beta}{2}}=\frac{\cos\frac{\alpha}{2}\cos\frac{\beta}{2}}{\cos\frac{\alpha}{2}\cos\frac{\beta}{2}}=1$