1. Алгебра
  2. Докажите что если a+b+c+d=4

Докажите что если a+b+c+d=4 то тогда 1/a^2+1/b^2+1/c^2+1/d^2>=4

marimitul marimitul    1   28.06.2021 21:36    0

Ответы
Marshall123 Marshall123  28.07.2021 22:28

Сразу скажем, что в таком виде результат неверен, более того, сумму квадратов обратных величин можно сделать сколь угодно близкой к нулю. Например, 104-100+100-100=4, а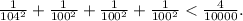 \frac{1}{104^2}+\frac{1}{100^2}+\frac{1}{100^2}+\frac{1}{100^2}

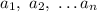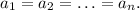
А вот если все четыре числа положительны, требуемое неравенство легко выводится из неравенства Коши между средним арифметическим и средним геометрическим: для неотрицательных a_1,\ a_2,\ \ldots a_n справедливо неравенство \frac{a_1+a_2+\ldots +a_n}{n}\ge \sqrt[n]{a_1\cdot a_2\cdot \ldots \cdot a_n}, причем неравенство превращается в равенство только в случае a_1=a_2=\ldots =a_n.

Из условия a+b+c+d=4 и неравенства Коши (если a, b, c, d положительны) следует, что 1=\frac {a+b+c+d}{4}\ge \sqrt[4]{a\cdot b\cdot c\cdot d}. Иными словами,

\sqrt[4]{abcd}\le 1. Чтобы дальше была комфортная жизнь, перепишем это в виде \frac{1}{\sqrt[4]{abcd}}\ge 1.

Из неравенства Коши следует, что

\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}+\frac{1}{d^2}\ge 4\sqrt[4]{\frac{1}{a^2b^2c^2d^2}}=\frac{4}{(\sqrt[4]{abcd})^2}\ge \frac{4}{1^2}=4,

что и требовалось доказать.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Fomabarca Fomabarca  29.11.2021 16:38
Решить уравнения: 1/6x=18, 7x+11,9=0, 6x-0,8=3x+1,1 Жду. Задача: Весь путь в 600 км турист пролетел на самолете и проехал на автобусе. На самолете он проделал путь на 190 км больше...
минам2003 минам2003  12.07.2019 12:20
Модуль х+7 равняется х+7 и 7+х или как?...
kkkkksss kkkkksss  12.07.2019 12:20
4целых 2/9 × 18 -6 целых 1/7 ÷ 1/7 вычислить...
dazacyhko dazacyhko  12.07.2019 12:20
Легкий вопрос, что-то ! ! 1) х²-3х/2=-1 2) х²-3х/2=2...
olesyakondakova olesyakondakova  12.07.2019 12:20
Вромбе mnkt угол n равен 60 градусов, mk= 10,5 см. найдите периметр ромба...
кисикмиксер кисикмиксер  12.07.2019 12:20
Докажите, что значение 25^5-125^3 кратно 4....
dianadidi3 dianadidi3  12.07.2019 12:20
Вычислить интеграл s(п; -п) cosx/2 dx...
Натальяроссия Натальяроссия  12.07.2019 12:20
8класс. 1. решите уравнение, применяя теорему обратную т. виета: x²-16x+63=0 2. один из корней уравнения x²+10x+q=0 равен -12. найдите другой корень и р....
MuertoLegend MuertoLegend  09.10.2019 11:06
Раздел многочлены выражение станднартный вид многочленастепень многочлена​...
ЭвелинаРожкова ЭвелинаРожкова  09.10.2019 11:05
Проходит ли ось симметрии параболы y=x^2-10x через точку: 1) (5; 10); 2) (3; -8); 3) (5; 0); 4) (-5; 1)? напишите решения ! ​...

Популярные вопросы