Докажите, что 1) сумма пяти последовательных натуральных чисел делится на 5
2)сумма четырех последовательных натуральных чисел не делится на 4
3 )сумма четырех последовательных и нечётных чисел делится на 8
4 )сумма четырёх последовательных четных натуральных чисел делится на 4
Другие вопросы по теме Алгебра
Популярные вопросы
- 1. ich … student. 2. du … lehrerin. 3. er … bauer. 4. sie … ärztin. 5. es …...
1 - Написать психологический портрет (т.е темперамент и акцентуация) персонажа из...
3 - При каком значении p один из корней уравнения x^2-px+6=0 равен единице? в этом...
3 - Определите знак выражения sin a * cos a * tg a * ctg a ; a) a = -189°; б) а...
3 - Вычислите площадь квадрата со стороной 2/9 см....
1 - ответь на вопросы после текста! introduction to the the internet millions of...
3 - Мне нужна схема present simple и present continios...
1 - Заданы уравнение двух тел x1=4+3t x2=1+6t найти место и время этих тел двумя...
2 - Сделать ! диктант осень. лес украсился в жёлтые, красные, золотистые цвета....
1 - Написать психологический портрет (темперамент, акцентуация) персонажа из фильма...
2
Если каждое слагаемое делится на некоторое число, то и вся сумма делится на это число.
Если одно слагаемое делится на некоторое число, а другое слагаемое не делится на это число, то и вся сумма не делится на это число.
1.
Пусть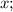
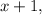
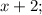
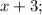
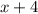 - пять последовательных натуральных чисел, тогда их сумма равна:
- пять последовательных натуральных чисел, тогда их сумма равна:
Очевидно, что каждое слагаемое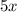 и
и 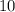 делится на 5, а это означает, что вся сумма делится на 5.
делится на 5, а это означает, что вся сумма делится на 5.
Доказано.
2.
Пусть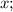
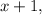
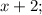
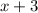 - четыре последовательных натуральных числа, тогда их сумма равна:
- четыре последовательных натуральных числа, тогда их сумма равна:
Очевидно, что первое слагаемое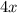 делится на 4, а второе слагаемое
делится на 4, а второе слагаемое 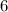 не делится на 4, это означает, что вся сумма не делится на 4.
не делится на 4, это означает, что вся сумма не делится на 4.
Доказано.
3.
Пусть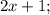
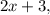
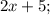
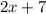 - четыре последовательных нечётных натуральных числа, тогда их сумма равна:
- четыре последовательных нечётных натуральных числа, тогда их сумма равна:
Очевидно, что каждое слагаемое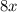 и
и 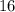 делится на 8, а это означает, что вся сумма делится на 8.
делится на 8, а это означает, что вся сумма делится на 8.
Доказано.
4.
Пусть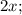
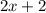 ;
; 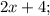
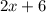 - четыре последовательных чётных натуральных числа, тогда их сумма равна:
- четыре последовательных чётных натуральных числа, тогда их сумма равна:
Очевидно, что каждое слагаемое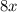 и
и 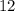 делится на 4, а это означает, что вся сумма делится на 4.
делится на 4, а это означает, что вся сумма делится на 4.
Доказано.