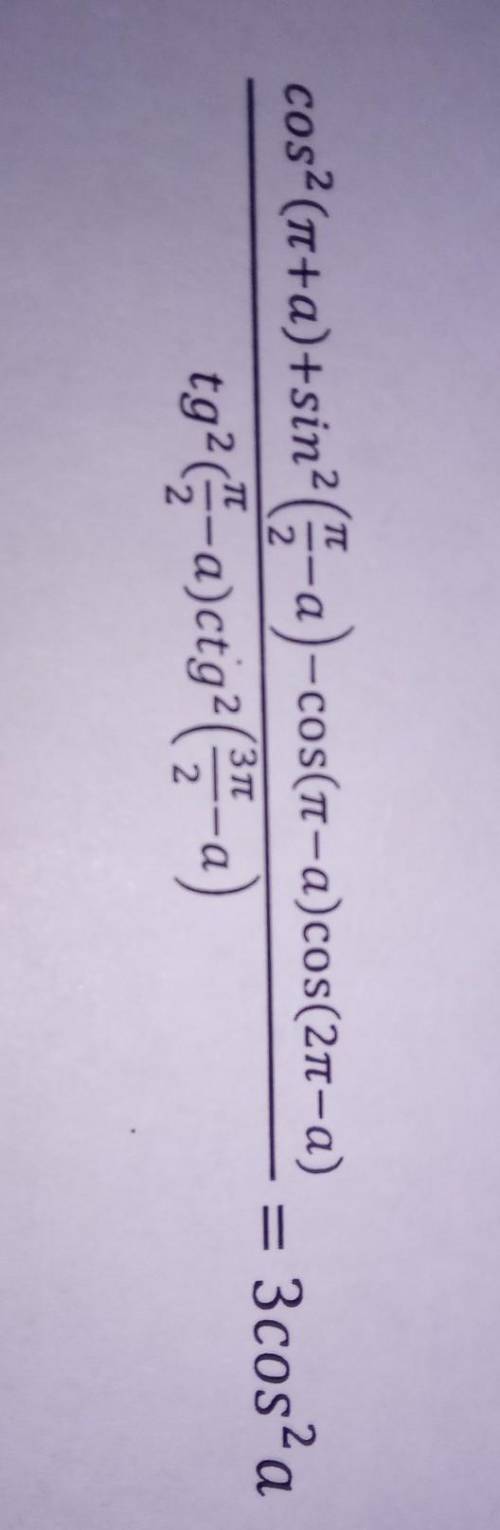
Докажи тождество :ᅠᅠᅠᅠᅠᅠᅠᅠ
Другие вопросы по теме Алгебра
Популярные вопросы
- Приставки с существительными когда слитно когда нет (чёт забыл)...
3 - На западном пути стоят 36 товарных и 24 пассажирских вагона. длина пассажирского...
2 - Напишите формулу ве-ва -2-метилпентаново-этиловый эфир...
2 - 6класс. я в теме не сильно разобралась, ! 1)решите уравнение 5*(х+1,2)=12,5х...
2 - Сколько звуков с в поговорке был бы покос да пришел мороз...
2 - Выпиши из данных слов, слова,в которых по два мягких согласных звука. весело,воробей,ворона,девочка,дежурный,деревня,заяц,карандаш,класс,корова,лисица,мальчик,машина,медведь,молоко,пальто,пенал,работа,,собака,сорока,тетрадь,ученик,ученица,учитель,учительница,хорошо,язык....
2 - На какие вопросы отвечают имена существительные...
1 - Выполнить синтаксический разбор предложения, обозначить части речи. а над речкой...
3 - Карточка №100в скитания пьера.чего желал пьер более всего, после того как покинул...
1 - Написать мини сочинение (5-6 предложений) на тему без нет будушего...
3
по формулам приведения
cos(π+α)=-cosα , cos²(π+α)=(-cosα )²= cos²α
sin(π/2+α)=cosα , sin²(π/2+α)=cos²α
cos(π-α)=-cosα
cos(2π-α)=cos(-α)=cosα
tg(π/2-α)=ctgα , tg²(π/2-α)=ctg²α
ctg(3π/2-α)=tgα ,ctg²(3π/2-α)=tg²α
теперь все закидываем в дробь
Для того, чтобы доказать тождество, преобразуем левую часть равенства , применяя формулы приведения.