Докажіть,що коли a^2 + b^2 + c^2 = ab + bc + ac , де a,b,c - дійсні числа,то a=b=c
Другие вопросы по теме Алгебра
Популярные вопросы
- По технической механике. удлинение стального стержня диаметром 5,5 см и длиной...
2 - Престройте предложение так чтобы подлежащее стало обращением. откуда-то клич...
1 - Ix. complete the sentences (1-5) with the most suitable preposition (a-e):...
2 - Плз, я даун, ниче понимаю в . можете перевести? нормально . я имею навыки работы...
3 - Решите это -7 класс, решить ну дно только пункты в) из каждого , решите что...
3 - (1-i)², (1-i)^10 выполнить комплексные вычисления с описанием...
2 - Ведут ночной образ жизни, не требовательны к пище и воде, быстро бегают, имеют...
1 - Мне нужно сочинение на тему жизнь петра в белгородской крепости (капитанская...
2 - Составьте уравнение касательной к графику функции y=4/3x^3/4+x^-3 в точке х=1...
2 - Тело упало с высоты 100 метров.найти за какое время оно вторую половину своего...
3
Возможно, существует и другой метод доказательства, но я буду использовать метод от противного.
Итак, нужно доказать, что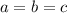 , то есть
, то есть
Перепишем наше равенство, переместив все в левую часть:
1) Предположим, что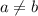 (при этом подразумевая, что
(при этом подразумевая, что 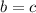 )
)
Тогда получаем следующее:
Далее смотрим: слева неотрицательное выражение всегда, а справа может быть и отрицательное, но у нас по условию дано, что для любых действительных чисел равенство выполняется, а здесь это далеко не так (на языке математики запись такая: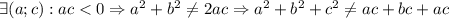 )
)
Возможно, это не очень явно, поэтому вспомним, что по предположению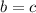 , и доделаем:
, и доделаем:
А это прямо яркий пример противоречия: предположив, что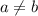 , мы получили
, мы получили 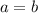 .
.
Из этого следует, что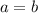 , но и из предположенного же
, но и из предположенного же 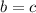 уже следует, что
уже следует, что 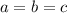 .
.
Вообще, по идее, этого уже достаточно, ну на всякий случай посмотрим ещё:
2) Предположим, что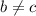 (при этом
(при этом 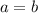 )
)
И тогда уже точно исходя из пунктов 1) и 2), получаем