Доказать справедливость неравенств |a+b| меньше либо равно |a|+|b|
Другие вопросы по теме Алгебра
Популярные вопросы
- по геометрии буду благодарен)...
3 - 1.24 Определите, будет ли равна сумма масс 6 протонов и 6 нейтронов...
1 - В трёх пронумерованных пробирках содержатся растворы:карбоната натрия,хлорида...
1 - вставить a/an или the I don t usually like staying at___ hotels,...
3 - Вычислите сумму геометрической прогрессии...
3 - При каком значении переменной равна нулю алгебраическая дробь...
1 - Допишіть праві частини рівнянь реакцій: S + О 2 → S + Н 2 → Складіть...
2 - Укажи ряд веществ, в котором записаны названия веществ, относящихся...
2 - Решите систему неравенст ...
2 - 1) Какими правами человека, гарантированными Конституцией РФ, Вы...
3
Можно скажем возвести в квадрат, тогда получим
Применяя это свойство модуля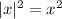
После приведения подобных останется
ab ≤ |a||b|
Произведение |a||b| всегда положительно при любых a и b
А произведение ab может быть как положительным (к примеру a>0, b>0 или a<0, b<0), так и отрицательным (a>0, b<0 или a<0, b>0)
В итоге, что и требовалось доказать |a+b|≤ |a|+|b|.
доказать можно, применим свойство модуля: |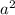 |=
|=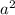 , то есть возведем обе части неравенства
, то есть возведем обе части неравенства  в квадрат:
в квадрат:
так как модуль - положительное число (из определения), то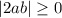 , в то время как 2ab может принимать различные значения: как польжительные, так и отрицательные, следовательно
, в то время как 2ab может принимать различные значения: как польжительные, так и отрицательные, следовательно 