1. Алгебра
  2. Доказать, что выражение x в квадрате

Доказать, что выражение x в квадрате +8x+18 принемает положительное значение при любом x.какое наименьшее значение принемает это выражение и прикаком x?

molchanets98p085or molchanets98p085or    2   31.03.2019 07:00    0

Ответы
kudzhan kudzhan  27.05.2020 21:09

Дискриминант меньше нуля;

(х+4)^2+2;

Наименьшее значение 2

ПОКАЗАТЬ ОТВЕТЫ
ЯСоваНоТупая ЯСоваНоТупая  27.05.2020 21:09

Рассматривается выражение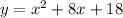 y = x^2 + 8x + 18

 

Докажем, что y положительно при любом значении x. Допустим, что это не так. Найдём такие x, при которых y ≤ 0. Для этого решим неравенство:

 

x^2 + 8x + 18 \leq 0 \Leftrightarrow x^2 + 8x + 16 + 2 \leq 0 \Leftrightarrow \left(x + 4\right)^2 + 2 \leq 0

 

Или

 

\left(x + 4\right)^2 \leq -2

 

Что не имеет решений, так как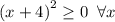 \left(x + 4\right)^2 \geq 0 \;\; \forall x

 

Мы пришли к противоречию. Следовательно,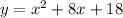 y = x^2 + 8x + 18 принимает положительное значение при любых x.

 

Для нахождения наименьшего значения найдём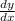 \frac{dy}{dx}:

 

\frac{dy}{dx} = 2x + 8

 

Приравняв его 0, найдём точку экстремума:

 

2x + 8 = 0 \Rightarrow x = -4

 

Убедимся, что найденная точка — действительно минимум.

 

\frac{dy}{dx}|_{x=-5} = -10 + 8 = -2 < 0

 

\frac{dy}{dx}|_{x=-3} = -6 + 8 = 2 0

 

Итак, первая производная меняет в точке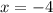 x = -4 знак с "-" на "+", следовательно, в этой точке мы действительно имеем минимум.

 

Значение y при x = -4:

 

y|_{x=-4} = (-4)^2 + 8 \cdot (-4) + 18 = 2

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Strelok72 Strelok72  28.08.2019 09:10
Определите 1-ый член и разность арифметической прогрессии: а11=6, а20=12...
viktorialychykowtuu4 viktorialychykowtuu4  28.08.2019 09:10
А) коля и петя проплыли на моторной лодке от пристани на некоторое расстояние вверх по течению реки, затем причалили к берегу и, порыбачив 3 часа, вернулись обратно через...
Shishmariya Shishmariya  28.08.2019 09:10
Откуда берутся плюсы и минусы в решении квадратных неравенств методом интервалов? расскажите!...
Ембергенова Ембергенова  28.08.2019 09:10
При каких значениях а корень уравнения 7*х + 12= 6 + а является числом большим 7 ?...
damirpernebek7 damirpernebek7  28.04.2020 16:51
очень нужно❤️какая из точек принадлежит графику функции y=15/xA(3;5)B(5;5)c(15;2)​...
Hennesy322 Hennesy322  28.04.2020 16:51
Если задуманное двузначное число сложить с суммой его цифр, то получится 90. Если же из задуманного двузначного числа вычесть 63, то получится двузначное число, записанное...
Pahnet Pahnet  28.04.2020 17:23
Коренем рівняння (х-34)-10=38 є число:...
Лейла5225 Лейла5225  22.05.2020 11:48
У выражение. — (10x +4,4y) - (-11y — 2,9x) =...
mickeymouse1958 mickeymouse1958  21.05.2020 11:38
Ребят решить контрольную работу по алгебре умоляю. ​...
рита429 рита429  21.05.2020 11:38
Произведение корней уравнения x квадрате минус 12 равно X X 2 - 1/2 равно икс равно ​...

Популярные вопросы