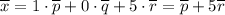Доказать, что векторы p={1,3,1}, q={7,-1,4}, r={-1,2,3} базис и разложить x={-4,13,16} за этим базисом. левую или правую тройку они ?
за !

Ответы

nastua89723 10.10.2020 12:05

Перепишем векторное уравнение в матричном виде

$\left(\begin{array}{ccc}1&7&-1\\3&-1&2\\ 1&4&3\end{array}\right|\left\begin{array}{ccc}-4\\13\\16\end{array}\right)$

Проверим создают ли заданные векторы базис. Для этого найдем определитель матрицы

$\left|\begin{array}{ccc}1&7&-1\\3&-1&2\\1&4&3\end{array}\right|=1\cdot (-1)\cdot 3+7\cdot 2\cdot 1+3\cdot 4\cdot (-1)-(1\cdot (-1)\cdot (-1)+\\ \\ +7\cdot 3\cdot 3+4\cdot 2\cdot 1)=-73\ne0$

Поскольку определитель матрицы не равен нулю, то данная система векторов является базисом.

От второй строки отнимем первую строку, умноженной на 3 и от третьей строки отнимем первую строку

$\left(\begin{array}{ccc}1&7&-1\\ 0&-22&5\\ 0&-3&4\end{array}\right|\left\begin{array}{ccc}-4\\25\\20\end{array}\right)$

От первой строки отнимем вторую строку , умноженной на (-7/22). Сложим третью строку и вторую строку, умноженной на 3

$\left(\begin{array}{ccc}1&0&\frac{13}{22}\\ 0&1&-\frac{5}{22}\\ 0&0&\frac{73}{22}\end{array}\right|\left\begin{array}{ccc}\frac{87}{22}\\ -\frac{25}{22}\\ \frac{365}{22}\end{array}\right)$

Заранее поделим третью строку на 73/22. Далее от первой строки отнимем третью строку, умноженной на 13/22; сложим вторую строку и третью строку, умноженной на 5/22

$\left(\begin{array}{ccc}1&0&0\\ 0&1&0\\ 0&0&1\end{array}\right|\left\begin{array}{ccc}1\\0\\5\end{array}\right)$