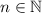Доказать, что при любом натуральном n число 10-(4^n)+3n делится на 9.
Другие вопросы по теме Алгебра
Популярные вопросы
- Явас умоляю! 1. 2 sin в квадрате x sin x - 1 = 0 2.3 cos в квадрате x - sin x +...
1 - Какой отличный признак человека отсутствует в перечне? человек к творчеству, умеет...
3 - Катер плыл 3,5 ч по течению реки и 0,6 ч по озеру. найдите путь, пройденный катером...
3 - Цель реформ избранной рады являлось а)упорядочить страной б)укрепить центральную...
3 - 4cos^2 x - 12*cos x + 5 = 0 корни пренадлежащие отрезку [-п; (5 *п)\2]...
1 - Эссе, по оо на тему: подростковая жизнь!...
2 - Втреугольнике abc угол с равен 90, ch-высота. ав=27, sina=2/3. найти ah. решить....
1 - 18a²z² 36a(2b-1)³z² сократите дробь: )...
3 - Тело движется по закону x(t)=t^4+t^2-3t.найдите ускорение тела через 2 с после начала...
2 - Расстояние между пунктами а и в равно 168км. товарный поезд проходит это расстояние...
2
Докажем методом математической индукции.
1) База индукции: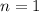
2) Предположим, что и для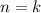 выражение
выражение 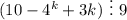
3) Индукционный переход: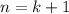
Первое слагаемое делится на 9 по второму пункту и второе слагаемое делится на 9, так как имеет сомножитель 9.
То есть,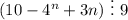 при
при