Доказать, что при любом n ∈ N (принадлежность):
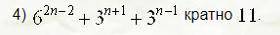
Другие вопросы по теме Алгебра
Популярные вопросы
- , 3. Яку роботу виконав газ, якщо він отримав 60Дж теплоти, а йоговнутрішня енергія...
2 - Риб яче життя знає річка а пташині думи розуміє вітер повний синтаксичний розбірпо...
1 - 35-100 %20-х Знайти -х у відсотках...
2 - Заполните пропуски в тексте. территория Краснодарского края находится в зоне...
1 - Вийдеш- це доконаний чи недоконаний вид...
3 - Скласти загальне питання до речення : Henry started at a new school two months...
2 - Легкий вопрос) Почти просто так ! Как это *позначити відмінок?*...
3 - Укажіть місце елемента в періодичній системі за його формулою 3s²3p²...
3 - Составить вопросы к каждому слово из кроссворда...
3 - Реши задачу, пошагово выполняя указанные действия. Определи, на сколько градусов...
3
Такую задачу можно решать методом математической индукции, а можно и по-другому. Поскольку в условии ничего не сказано, как нужно решать, будем решать по-другому.
Множитель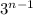 не влияет на делимость на 11, забудем про него.
не влияет на делимость на 11, забудем про него.
Объяснение: если n=1⇒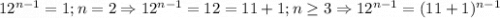
получается перемножением кучи скобок, во всех произведениях будет хотя бы один множитель 11, и только одно произведение является произведением единиц. Другой объяснения основывается на биноме Ньютона, третий использует сравнения.
Решение : //////////////////////////////////