1. Алгебра
  2. Доказать, что при каждом

Доказать, что при каждом n ∈ N (принадлежность) верно равенство:


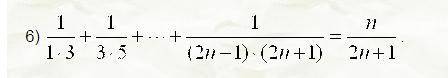
Доказать, что при каждом n ∈ N (принадлежность) верно равенство:

popovaliliya popovaliliya    1   24.06.2021 13:22    2

Ответы
Sashakosix Sashakosix  24.07.2021 13:24

Воспользуемся формулой

\frac{1}{n(n+k)}=\frac{1}{k}(\frac{1}{n}-\frac{1}{n+k}),

которая проверяется непосредственно.

В частном случае, когда k=2, получаем формулу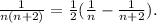  \frac{1}{n(n+2)}=\frac{1}{2}(\frac{1}{n}-\frac{1}{n+2}). Поэтому данная нам сумма может быть записана в виде

\frac{1}{2}(\frac{1}{1}-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\ldots \frac{1}{2n-1}-\frac{1}{2n+1})= \frac{1}{2}(1-\frac{1}{2n+1})=\frac{n}{2n+1}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
ЕмелиЯна ЕмелиЯна  23.12.2020 19:42
Знайдіть множину значень функції у=сosx+1​...
маша4737 маша4737  23.12.2020 19:41
Знайти область визначення функції ​...
301222 301222  23.12.2020 19:41
Определи цену деления шкалы термометра 37° 23°​...
miravolkova19 miravolkova19  23.12.2020 19:41
сколько будет 0.6 во второй степени?!​...
anton4rf4 anton4rf4  26.05.2019 23:10
Для данного линейного уравнения 7x-4y-8=0 найдите значение у,соответствующие значению х=4 с решением,напишите решение...
nastyauymionova nastyauymionova  26.05.2019 23:10
2.7грамм на сантиметр в кубе перевести в килограмм на метр в кубе...
hopesegul hopesegul  26.05.2019 23:10
2sin в квадрате альфа +cos 2альфа заранее ! )...
Hjlüüä Hjlüüä  26.05.2019 23:10
Доказать,что81 в 31степени минус9 в 60 степени делится на 6480.(мне нужно полный цикл решения)....
denjis denjis  26.05.2019 23:10
По ! надо доказать неравенство. a/b + b/a ≥ 2...
sofiko365 sofiko365  26.05.2019 23:10
Надо докажите тождество (4-7z)(5z-+3z)(z-5)= -2(19z^2-6)+45z...

Популярные вопросы