Доказать что n(3)+5n делится на 6 при любом натуральном n.

Question

Алгебра: Доказать что n(3)+5n делится на 6 при любом натуральном n.

OlegBasov · Answer

n^3+5n=n(n^2+5)

1) Делимость на 2: очевидно (при четном n четно первое слагаемое, при нечетном - второе).

2) Делимость на 3: есть три варианта, рассмотрим каждый из них.

а) n делится на 3 -> очевидно, всё делится на 3

б) n=3k+1: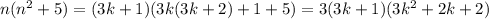 n(n^2+5)=(3k+1)(3k(3k+2)+1+5)=3(3k+1)(3k^2+2k+2) -> делится на 3

в) n=3k-1: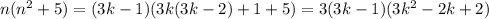 n(n^2+5)=(3k-1)(3k(3k-2)+1+5)=3(3k-1)(3k^2-2k+2) -> делится на 3

Число в любом случае делится на 2 и 3 -> делится на 6.