Доказать, что многочлен f(x,y,z) = x3+y3+z3 - xyz
нельзя представить в виде произведения многочленов
первой степени с действительными коэффициентами.

Другие вопросы по теме Алгебра
Популярные вопросы
- Квадрата равна 64 дм в квадрате найди площадь прямоугольника периметр...
2 - Найдите значение выражения 32x^4y при x= -1/2, y= 7...
2 - Можете перевести текст на язык, любимые игрушки наших родителей...
3 - Краткая справка о екатерине второй...
3 - Уздорово человека- хорошая кожа, при стрессе и болезни состояние...
2 - Взять любой мультик и доказать, что это искусство по признакам,какой...
3 - Какая гора в древней греции самая большая...
3 - Когда ветер становится сильным рекомендуют опустить паруса .как...
1 - По мальнькому принцу, что я хотел бы сказать маленькому принцу....
3 - Одна вторая часть 1)от 10 см или одна пятая часть от 20 см 2)...
2
Пусть дан многочлен:
Предположим, что его можно представить в виде произведения многочленов первой степени с действительными коэффициентами.
Многочлен первой степени имеет вид:
Поскольку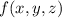 не содержит свободного члена, то хотя бы один из свободных членов в одном из множителей равен
не содержит свободного члена, то хотя бы один из свободных членов в одном из множителей равен 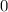 .
.
Но тогда, существует такая линейная комбинация:
При которой данный многочлен тождественно равен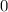 .
.
Попробуем найти такую комбинацию:
Мы пришли к противоречию, это невозможно.