Доказать, что функцию с модулями можно представить в виде...

Другие вопросы по теме Алгебра
Популярные вопросы
- Фонетический разбор: сквозь морфемный разбор: подводный синтаксический разбор:...
1 - Постепенно льдинка оборачивалась в светлую каплю освежая и питая собою цветок...
3 - Сравните числа: 1) 6,7 и 6,8 2) 5,4 и 4,9 3) 12,4 и 12,42 4) 26,39 и 26,279 5)...
3 - Умение владеть правой рукой у человека доминирует над леворукостью, а нормальное...
1 - Сколько натуральных чисел n следующим свойством: число n можно представить ровно...
3 - Каким словом можно заменить слово старый вот предложение васька не на шутку перепугался:...
3 - 1.определите объём стальной плиты,полностью погруженной в воду,если на неё действует...
3 - 20б (больше у меня нету турист планировал пройти за первые три для 3/5 всего маршрута....
2 - Iwill ring you when i get to the airport нужно will или его нужно убрать?...
3 - Втреугольнике авс сторона вс=35 см,∠в=40,∠с=80.найдите угол а и стороны ав,ас....
1
Проведем доказательство индукцией по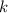 .
.
База: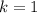 .
.
Имеем два промежутка:![(-\infty,\; x_{1}]](/tpl/images/1359/4865/5423e.png) и
и  . Докажем, что существует представление
. Докажем, что существует представление 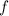 в виде
в виде 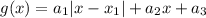 . Для этого достаточно доказать, что функция
. Для этого достаточно доказать, что функция  линейна на каждом из указанных промежутков и производная (угол наклона прямой) может принимать любые численные значения. Линейность функции очевидна. Рассмотрим
линейна на каждом из указанных промежутков и производная (угол наклона прямой) может принимать любые численные значения. Линейность функции очевидна. Рассмотрим  на промежутках:
на промежутках:
Единственность представления доказывается просто. Пусть нашлись другие (возможно совпадающие, но не полностью) числа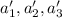 . Рассмотрим первый промежуток:
. Рассмотрим первый промежуток: 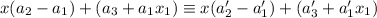 , откуда
, откуда 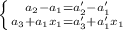 . К этой системе добавятся условия из второго промежутка:
. К этой системе добавятся условия из второго промежутка: 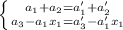 . Решая систему из первого уравнения первой системы и первого уравнения второй, получим
. Решая систему из первого уравнения первой системы и первого уравнения второй, получим 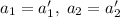 . Используя это равенство для второго уравнения первой системы, приходим к равенству
. Используя это равенство для второго уравнения первой системы, приходим к равенству 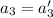 . Единственность доказана.
. Единственность доказана.
Переход: пусть для некоторого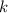 выполнено условие задачи. Докажем, что оно выполнено и для
выполнено условие задачи. Докажем, что оно выполнено и для 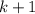 .
.
Рассмотрим функцию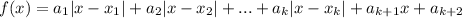 . По предположению индукции
. По предположению индукции 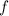 можно представить в этом виде, причем единственным образом. Рассмотрим следующую функцию
можно представить в этом виде, причем единственным образом. Рассмотрим следующую функцию  . Очевидно, что первые
. Очевидно, что первые 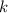 чисел можно подобрать по предположению индукции, представив тем самым функцию
чисел можно подобрать по предположению индукции, представив тем самым функцию 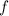 на промежутках
на промежутках ![(-\infty,\; x_{1}],\; [x_{1},\; x_{2}],\;...,\;[x_{k-1},\; x_{k}]](/tpl/images/1359/4865/94330.png) . Оставшуюся часть
. Оставшуюся часть ![[x_{k},\; x_{k+1}],\; [x_{k+1},\; \infty)](/tpl/images/1359/4865/b8679.png) представим, пользуясь базой индукции (при этом отсутствие минус бесконечности на ход решения не влияет). Докажем единственность. Пусть нашелся другой набор чисел
представим, пользуясь базой индукции (при этом отсутствие минус бесконечности на ход решения не влияет). Докажем единственность. Пусть нашелся другой набор чисел 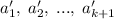 . Введем функцию
. Введем функцию 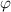 , которая описывается следующим графиком: она совпадает с
, которая описывается следующим графиком: она совпадает с 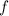 на первых
на первых 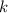 промежутках, а кусок прямой на
промежутках, а кусок прямой на 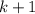 -ом продлевается в бесконечность (вправо). Тогда у
-ом продлевается в бесконечность (вправо). Тогда у 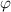 два представления, что противоречит предположению индукции. Следовательно,
два представления, что противоречит предположению индукции. Следовательно, 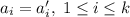 , причем
, причем 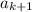 может отличаться от
может отличаться от 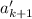 . Тогда проведем те же рассуждения, взяв последние
. Тогда проведем те же рассуждения, взяв последние 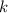 чисел.
чисел.