Доказать, что функция: y=2(x-3)^2 возрастает на промежутке [3; +∞)
Другие вопросы по теме Алгебра
Популярные вопросы
- Придумать предложения со словами heavy, sticky, very, lady, baby,...
1 - Перпендикулярны ли векторы n(9: 3) m(-4; 12...
2 - От каких животных произошли древние рыбы обоснуйте свой ответ !...
2 - Решить линейное уравнение! 1) 3(x+5)=7-5x 2) 19(y-9)=3(у+7) 3) 4(x-9)=3(x-8)...
1 - Верно ли что две пятых равно: 1)2+5; 2)5-2; 3)2*5; 4)2: 5?...
1 - Дано три числа а,в,с. возвести в квадрат те числа которые отрицательные....
1 - Напишите сочинение на тему .рассказать о том чему он тебя научил....
2 - Надо зделать предложение 1 повествовательное не восклицательное простое...
2 - Жұмбақ: ағайынды жетеуінің бесеуінің жұмысы бар екеуінің жұмысы жоқ,...
2 - Отрезок соединяющий две точки поверхности шара и проходящий через...
1
y=2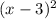 - раскроем скобки
- раскроем скобки
y=2(x^2-6x+9)
y=2x^2-12x+18
4x-12=0 - результат производной приравняем к нулю и решим уравнение.
4x=12
x=3
Подставим в производную люое число больше трех, получаем положителное значение. Подставим люьое число меньше трёх - отрицательное. Выходит функция возрастает на промежутке [3;+∞) .