Доказать, что для любого n число 7^2n-4^2n делится на

7^(2n) - 4^(2n) = (7^2)^n - (4^2)^n = 49^n - 16^n = (49 - 16)(49^(n-1)+ 49^(n-2)*16 + + 49*16^(n-2) + 16^(n-1)) = 33 * (49^(n-1) + + 16^(n-1))

в произведении один из множителей делится на 33, значит и все произведение делится на 33

ну и если 7^2*n - 4^2*n = 49n - 16n = 33n

аналогично

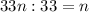, значит делится на 33 нацело

()