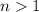Доказать, что число 2n^3-3n^2+n делится на 6 при любом n€n (n> 1)
Другие вопросы по теме Алгебра
Популярные вопросы
- Решите систему уравнений сложения { x+y=12 {x-y=2 15...
3 - Однажды к известному естествоиспытателю чарлзу дарвину пришли за советом фермеры.они...
3 - Равнобедренном треугольнике дек угол к =100 ка медиана найдите углы треуголька...
1 - Прочитайте стихотворение. запишите 5-6 словосочетаний, раскрывающих мысль автора....
3 - Мотоциклист ехал 0,8 ч по асфальтированной дороге ,и 0,7 ч по грунтовой дороге...
2 - Оля выстираладля куклы 4платья искать оля выстерала для куклы 4 платья а кофточек...
2 - Решить самостоятельную по 8класс 1) 6x 12 2) -5x≤-10 3) 4x+6 2x+10 4) 2(x+1)-1≥6(x+4)-3...
3 - Запишите всю программу на языке html для получения следующей web-страницы 1....
1 - Написать дневник главного героя рассказа уроки французского...
3 - Какому прзднику посвятил свое произведение рахманинов?...
2
Докажем методом математической индукции
1) База индукции: n = 2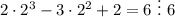
2) Предположим что и для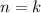 выражение
выражение 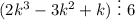
3) Индукционный переход: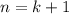
Первое слагаемое делится по предположению (пункт 2), ну а второе слагаемое делится на 6 тоже, т.к. имеется сомножитель 6. Следовательно,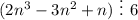 для всех натуральных
для всех натуральных 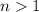
Второй
Разложим данное выражение на множители
Среди двух последовательных чисел обязательно найдется четное и нечетное числа и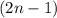 - нечетное, поэтому
- нечетное, поэтому 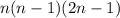 делится на 6 при натуральных
делится на 6 при натуральных