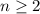Доказать, что 7 в степени n>6n+5, где n принадлежит N, n>=2
Другие вопросы по теме Алгебра
Популярные вопросы
- Решить уравнение 4х квадрате минус5х = 0...
2 - №67 разгадайте кроссворд система объектов 1.система входящая в состав другой...
2 - ответ на загадку: ерте тұрдым, екі айыр жолға түстім...
1 - Гражданин приобрел в автосалоне автомобиль и застраховал его. отношения гражданина...
2 - Как построить график функции: у= корень квадратный из х и все это в я правильно...
3 - Вчем была основная трудность при чтении египетских иероглифов?...
2 - Найдите корни уравнения : 11x²-6x+3=0, -7x²+13x+9=-9+13x...
3 - Ранняя весна составить сложное прилагательное...
1 - Put the verbs in the correct tenses. 7)-you (fly) to the sea or (go) by train?...
2 - Обширный устойчивый антициклон устанавливается зимой: 1) в центральной россии;...
2
Докажем методом математической индукции
1) n = 2: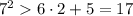 - верно
- верно
2) Предположим, что и при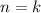 верно неравенство
верно неравенство 
3) Индукционный переход
Очевидно, что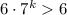 и
и  (по предположению), то сложив эти неравенства, получим
(по предположению), то сложив эти неравенства, получим 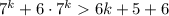 , т.е. третий пункт выполнено. Следовательно, на основании метода математической индукции делаем вывод, что неравенство
, т.е. третий пункт выполнено. Следовательно, на основании метода математической индукции делаем вывод, что неравенство 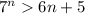 верно для всех натуральных
верно для всех натуральных